题目内容
10.①($\sqrt{48}$+$\sqrt{20}$)+($\sqrt{12}$-$\sqrt{5}$)②(2$\sqrt{48}$-3$\sqrt{27}$)÷$\sqrt{6}$.
分析 ①先把各二次根式化为最简二次根式,然后去括号后合并即可;
②先把各二次根式化为最简二次根式,然后把括号内合并后进行二次根式的除法运算.
解答 解:①原式=4$\sqrt{3}$+2$\sqrt{5}$+2$\sqrt{3}$-$\sqrt{5}$
=6$\sqrt{2}$+$\sqrt{5}$;
②原式=(8$\sqrt{3}$-9$\sqrt{3}$)÷$\sqrt{6}$
=-$\sqrt{3}$÷$\sqrt{6}$
=-$\frac{\sqrt{2}}{2}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
5.在平面直角坐标系中,若点P(m,1)在第二象限,则点Q(-m,0)在( )
| A. | x轴正半轴上 | B. | y轴正半轴上 | C. | x轴负半轴上 | D. | y轴负半轴上 |
15.立方根等于它本身的所有数为( )
| A. | -1,0,1 | B. | 0,1 | C. | 0,-1 | D. | 1 |
19.下列命题中的假命题是( )
| A. | 同位角相等,两直线平行 | B. | 内错角相等,两直线平行 | ||
| C. | 同旁内角互补,两直线平行 | D. | 对顶角相等,两直线平行 |
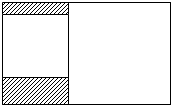 如图所示,某工人师傅要在一个面积为15m2的矩形钢板上裁剪下两个相邻的正方形钢板当工作台的桌面,且要使大正方形的边长比小正方形的边长大1m.求裁剪后剩下的阴影部分的面积.
如图所示,某工人师傅要在一个面积为15m2的矩形钢板上裁剪下两个相邻的正方形钢板当工作台的桌面,且要使大正方形的边长比小正方形的边长大1m.求裁剪后剩下的阴影部分的面积. 如图,已知⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.
如图,已知⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE. 如图,直线l1∥l2,AB⊥l1,垂足为D,BC与直线l2相交于点C,若∠1=35°,则∠2=125°.
如图,直线l1∥l2,AB⊥l1,垂足为D,BC与直线l2相交于点C,若∠1=35°,则∠2=125°.