题目内容
5．
如图，∠AOE=∠BOE=15°，EF∥OB，EC⊥OB，若EC=3，则EF的长为6．
分析 作EG⊥OA于G，根据角的平分线上的点到角的两边的距离相等求出EG=EC=3，根据平行线的性质和直角三角形的性质求出EF的长．
解答 
解：作EG⊥OA于G，
∵∠AOE=∠BOE，EC⊥OB，EG⊥OA，
∴EG=EC=3，
∵EF∥OB，
∴∠OEF=∠BOE=15°，
∴∠EFG=30°，
∴EF=2EC=6，
故答案为：6．
点评 本题考查的是角平分线的性质和直角三角形的性质，掌握角的平分线上的点到角的两边的距离相等和直角三角形的性质是解题的关键．
练习册系列答案
巧学巧练系列答案
相关题目
15．下列函数中是二次函数的有（ ）
①y=x+$\frac{1}{x}$；②y=3（x-1）2+2；③y=（x+3）2-2x2；④y=$\frac{1}{{x}^{2}}$+x．
①y=x+$\frac{1}{x}$；②y=3（x-1）2+2；③y=（x+3）2-2x2；④y=$\frac{1}{{x}^{2}}$+x．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
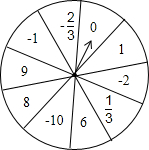如图是小明和小颖共同设计的自由转动的十等分转盘，上面写有10个有理数．
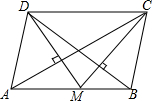点M在平行四边形ABCD的边AB上，满足AM：MB=4：3，且DM和CM分别垂直于AC和BD．若BC=5cm，请问?ABCD的面积是多少cm2？
20．若有一个n边形，其内角和大于它的外角和，则n的值至少为（ ）
| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
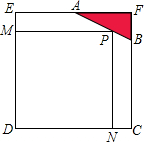已知边长为4的正方形截取一个角后成为五边形ABCDE（如图），其中AF=2，BF=1．若在AB上有一点P使矩形MPND的面积最大，请你求出此时矩形MPND的边长DN、PN．
如图，C是以AB为直径的⊙O上一点，过O作OE⊥AC于点E，过点A作⊙O的切线交OE的延长线于点F，连接CF并延长交BA的延长线于点P．