题目内容
7.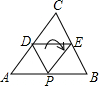 如图,D,E分别为△ABC的边AC,BC的中点,将此三角形沿DE折叠,使点C落在AB边上的点P处.若∠CDE=48°,则∠APD等于( )
如图,D,E分别为△ABC的边AC,BC的中点,将此三角形沿DE折叠,使点C落在AB边上的点P处.若∠CDE=48°,则∠APD等于( )| A. | 48° | B. | 50° | C. | 52° | D. | 58° |
分析 根据D、E分别为△ABC的边AC、BC的中点,即可得出DE为△ABC的中位线,进而可得出DE∥AB,再根据平行线的性质结合折叠的性质即可得出∠APD=∠PDE=∠CDE=48°,此题得解.
解答 解:∵D,E分别为△ABC的边AC,BC的中点,
∴DE为△ABC的中位线,
∴DE∥AB,
∴∠APD=∠PDE.
由折叠的性质可知:∠PDE=∠CDE=48°,
∴∠APD=48°.
故选A.
点评 本题考查了中位线的性质、平行线的性质以及翻折变换,根据翻折变换找出∠PDE=∠CDE=48°是解题的关键.

练习册系列答案
相关题目
17.三角形的角平分线、中线和高( )
| A. | 都是线段 | B. | 都是射线 | C. | 都是直线 | D. | 不都是线段 |
15.要了解全校2000名学生课外作业负担情况,你认为以下抽样方法中比较合理的是( )
| A. | 调查全体男生 | B. | 调查全体女生 | ||
| C. | 调查七年级全体学生 | D. | 调查各年级中的部分学生 |
19.下列说法正确的是( )
| A. | 将一个三角形沿一条边旋转一周,可以得到一个四边形 | |
| B. | 射线AB与射线BA是同一条射线 | |
| C. | 经过两点只能作一条直线 | |
| D. | 因为2<4,所以-2<-4 |
 如图是由36个边长为1的正方形组成的6×6网格,则格点多边形ABCDE的面积是11.
如图是由36个边长为1的正方形组成的6×6网格,则格点多边形ABCDE的面积是11.
 如图,在△ABC中,AB=AC=10,D是BC上一动点(D与B、C不重合),且DE∥AB,DF∥AC,则四边形DEAF的周长是( )
如图,在△ABC中,AB=AC=10,D是BC上一动点(D与B、C不重合),且DE∥AB,DF∥AC,则四边形DEAF的周长是( )