题目内容
17.三角形的角平分线、中线和高( )| A. | 都是线段 | B. | 都是射线 | C. | 都是直线 | D. | 不都是线段 |
分析 从三角形的一个顶点向底边作垂线,垂足与顶点之间的线段叫做三角形的高. 三角形一个内角的平分线与这个内角的对边交于一点,则这个内角的顶点与所交的点间的线段叫做三角形的角平分线.三角形一边的中点与此边所对顶点的连线叫做三角形的中线.
解答 解:三角形的角平分线、中线和高都是线段.
故选(A)
点评 本题主要考查了三角形的角平分线、中线以及高线的概念,解题时注意:三角形有三条中线,有三条高线,有三条角平分线,它们都是线段.

练习册系列答案
相关题目
7.如果两个有理数的和为零,那么这两个有理数( )
| A. | 互为相反数 | B. | 互为倒数 | C. | 有一个等于零 | D. | 无法确定 |
8.如图,能正确描述A到B到C的变换的是( )


| A. | A旋转135°后平移2cm,再平移2cm | B. | A旋转135°后平移4cm,再平移4cm | ||
| C. | A平移2cm后旋转135°,再平移2cm | D. | A平移2cm后旋转135°,再平移4cm |
5.已知点A(-2,y1),B(2,y2),C(3,y3)在抛物线y=x2-2x+c上,则y1,y2,y3的大小关系是( )
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y3>y2>y1 | D. | y2>y3>y1 |
12.下列度数中,不可能是某个多边形的内角和的是( )
| A. | 180° | B. | 270° | C. | 2700° | D. | 1800° |
2.“$\frac{9}{16}$的算术平方根是$\frac{3}{4}$”,用数学式子表示为( )
| A. | ±$\sqrt{\frac{9}{16}}$=$\frac{3}{4}$ | B. | $\sqrt{\frac{9}{16}}$=±$\frac{3}{4}$ | C. | $\sqrt{\frac{9}{16}}$=$\frac{3}{4}$ | D. | ±$\sqrt{\frac{9}{16}}$=±$\frac{3}{4}$ |
7.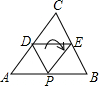 如图,D,E分别为△ABC的边AC,BC的中点,将此三角形沿DE折叠,使点C落在AB边上的点P处.若∠CDE=48°,则∠APD等于( )
如图,D,E分别为△ABC的边AC,BC的中点,将此三角形沿DE折叠,使点C落在AB边上的点P处.若∠CDE=48°,则∠APD等于( )
 如图,D,E分别为△ABC的边AC,BC的中点,将此三角形沿DE折叠,使点C落在AB边上的点P处.若∠CDE=48°,则∠APD等于( )
如图,D,E分别为△ABC的边AC,BC的中点,将此三角形沿DE折叠,使点C落在AB边上的点P处.若∠CDE=48°,则∠APD等于( )| A. | 48° | B. | 50° | C. | 52° | D. | 58° |
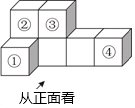 如图,是由7个大小相同的小正方体堆砌而成的几何体,若从标有①、②、③、④的四个小正方体中取走一个后,余下几何体与原几何体的主视图相同,则取走的正方体是( )
如图,是由7个大小相同的小正方体堆砌而成的几何体,若从标有①、②、③、④的四个小正方体中取走一个后,余下几何体与原几何体的主视图相同,则取走的正方体是( )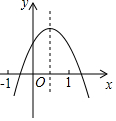 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b<0;③4a-2b+c<0;④a-c>0.其中正确结论的个数为( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b<0;③4a-2b+c<0;④a-c>0.其中正确结论的个数为( )