题目内容
12.如图,图案均是用长度相等的小木棒,按一定规律拼撘而成,第一个图案需4根小木棒,则第6个图案小木棒根数是54.
分析 由题意可知:第1个图案需要小木棒1×(1+3)=4根,第二个图案需要2×(2+3)=10根,第三个图案需要3×(3+3)=18根,第四个图案需要4×(4+3)=28根,…,继而即可找出规律,进一步求出第6个图案需要小木棒的根数
解答 解:拼搭第1个图案需4=1×(1+3)根小木棒,
拼搭第2个图案需10=2×(2+3)根小木棒,
拼搭第3个图案需18=3×(3+3)根小木棒,
拼搭第4个图案需28=4×(4+3)根小木棒,
…
拼搭第n个图案需小木棒n(n+3)=n2+3n根.
当n=6时,n2+3n=62+3×6=54.
故答案为:54.
点评 此题考查图形的变化规律,找出图形之间的联系,得出数字之间的运算规律,利用规律解决问题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
2.“$\frac{9}{16}$的算术平方根是$\frac{3}{4}$”,用数学式子表示为( )
| A. | ±$\sqrt{\frac{9}{16}}$=$\frac{3}{4}$ | B. | $\sqrt{\frac{9}{16}}$=±$\frac{3}{4}$ | C. | $\sqrt{\frac{9}{16}}$=$\frac{3}{4}$ | D. | ±$\sqrt{\frac{9}{16}}$=±$\frac{3}{4}$ |
7.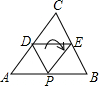 如图,D,E分别为△ABC的边AC,BC的中点,将此三角形沿DE折叠,使点C落在AB边上的点P处.若∠CDE=48°,则∠APD等于( )
如图,D,E分别为△ABC的边AC,BC的中点,将此三角形沿DE折叠,使点C落在AB边上的点P处.若∠CDE=48°,则∠APD等于( )
 如图,D,E分别为△ABC的边AC,BC的中点,将此三角形沿DE折叠,使点C落在AB边上的点P处.若∠CDE=48°,则∠APD等于( )
如图,D,E分别为△ABC的边AC,BC的中点,将此三角形沿DE折叠,使点C落在AB边上的点P处.若∠CDE=48°,则∠APD等于( )| A. | 48° | B. | 50° | C. | 52° | D. | 58° |
17.直线AB上有一点异于A、B的C,直线AB外有一点D,则A、B、C、D四点能确定的直线有( )
| A. | 3条 | B. | 4条 | C. | 1条或4条 | D. | 4条或6条 |
4.在直角坐标系中,已知点A(1,0),⊙A的半径是5,若点D(-2,a)在⊙A外,则a的范围是( )
| A. | a>4 | B. | a>4或a<-4 | C. | a<-4 | D. | -4<a<4 |
1.若等腰三角形的腰长为5cm,底长为8cm,那么腰上的高为( )
| A. | 12 cm | B. | 10 cm | C. | 4.8 cm | D. | 6 cm |
 如图,在△ABC中,AB=3,AC=4,BC=5,P为BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为2.4.
如图,在△ABC中,AB=3,AC=4,BC=5,P为BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为2.4.