题目内容
3.如图,菱形ABCD,∠A=60°,M,N分别在AD,DC上,且∠BMN=60°.(1)求证:BM=MN;
(2)若M,N分别在DA,CD的延长线,上述结论是否成立,请说明理由.
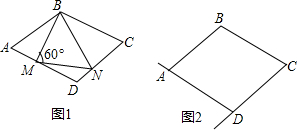
分析 (1)连接BD,先证明△ABD为等边三角形,得出∠ABD=60°,AB=BD,同理得出∠BDC=60°,证出∠NMD=∠ABM,证明M、D、N、B四点共圆,证出∠ABM=∠DBN,证明△AMB≌△DNB,即可得出结论;
(2)同(1)可证.
解答 (1)证明:连接BD,如图1所示: ∵四边形ABCD为菱形,
∵四边形ABCD为菱形,
∴AB=AD,
∵∠A=60°,
∴△ABD为等边三角形,
∴∠ABD=60°,AB=BD,
同理:∠BDC=60°,
∵∠BMD=60°+∠NMD=∠A+∠ABM,
∴∠NMD=∠ABM,
∵∠BMN=∠BDN=60°,
∴M、D、N、B四点共圆,
∴∠NMD=∠DBN,
∴∠ABM=∠DBN,
在△AMB和△DNB中,$\left\{\begin{array}{l}{∠ABM=∠DBN}&{\;}\\{∠A=∠BDN}&{\;}\\{AB=DB}&{\;}\end{array}\right.$,
∴△AMB≌△DNB(AAS),
∴BM=BN,
又∵∠BMN=60°,
∴△BMN为等边三角形,
∴BM=MN;
(2)成立;理由如下:如图2所示: 同(1)可证:B、M、N、D四点共圆,△AMB≌△DNB,
同(1)可证:B、M、N、D四点共圆,△AMB≌△DNB,
∴BM=BN,
∴△BMN是等边三角形,
∴BM=MN.
点评 本题考查了菱形的性质、全等三角形的判定与性质、等边三角形的判定与性质、四点共圆;本题难度较大;需要通过辅助线证明三角形全等和四点共圆才能得出结论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
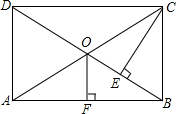 如图,矩形ABCD的对角线AC、BD相交于点O,CE⊥BD,且DE:EB=3:1,OF⊥AB于F,OF=3,求矩形对角线的长.
如图,矩形ABCD的对角线AC、BD相交于点O,CE⊥BD,且DE:EB=3:1,OF⊥AB于F,OF=3,求矩形对角线的长. 如图,抛物线y=ax2+1,y=ax2-1(a<0)的图象与直线x=-2,x=2所围成的阴影部分图形的面积是8.
如图,抛物线y=ax2+1,y=ax2-1(a<0)的图象与直线x=-2,x=2所围成的阴影部分图形的面积是8.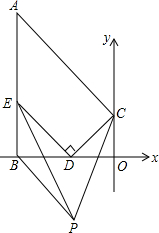 如图,直线x⊥直线y于点O,直线x⊥AB于点B,E是线段AB上一定点,D点为线段OB上的一动点(点D不与点O、B重合),CD⊥DE交直线y于点C,连接AC,∠BED、∠DCO的角平分线的交点为P.
如图,直线x⊥直线y于点O,直线x⊥AB于点B,E是线段AB上一定点,D点为线段OB上的一动点(点D不与点O、B重合),CD⊥DE交直线y于点C,连接AC,∠BED、∠DCO的角平分线的交点为P.