题目内容
9.(1)计算:($\sqrt{5}$-π)0-6tan30°+($\frac{1}{2}$)-2+|1-$\sqrt{3}$|.(2)解不等式组$\left\{\begin{array}{l}{4(x-1)≤3(x+2)}\\{\frac{x-1}{2}<x-4}\end{array}$,并写出它的所有整数解.
分析 (1)原式利用零指数幂、负整数指数幂法则,特殊角的三角函数值,以及绝对值的代数意义化简即可得到结果.
(2)分别求出各不等式的解集,再求出其公共解集,在其公共解集内找出符合条件的x的整数解即可.
解答 解:(1)原式=1-6×$\frac{\sqrt{3}}{3}$+4+$\sqrt{3}$-1
=4-$\sqrt{3}$;
(2)$\left\{\begin{array}{l}{4(x-1)≤3(x+2)①}\\{\frac{x-1}{2}<x-4②}\end{array}\right.$
解不等式①,得x≤10.
解不等式②,得x>7.
∴原不等式组的解集为7<x≤10.
∴原不等式组的所有整数解为8,9,10.
点评 本题考查的是解一元一次不等式组及一元一次不等式组的整数解,能利用数形结合求不等式组的解集是解答此题的关键.也考查了实数的运算,零指数幂、负整数指数幂.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
8.已知x2+kx+16是一个完全平方式,则k的值为( )
| A. | 4 | B. | 8 | C. | -8 | D. | ±8 |
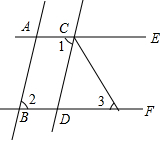 如图,已知AB∥CD,∠1=∠2,CF平分∠DCE.
如图,已知AB∥CD,∠1=∠2,CF平分∠DCE. 如图,在边长为1的小正方形组成的网格中,四边形ABCD的四个顶点都在格点上,请按要求完成下列各题.
如图,在边长为1的小正方形组成的网格中,四边形ABCD的四个顶点都在格点上,请按要求完成下列各题. 如图,在等腰直角三角形ABC中,∠ABC=90°,AB=BC=2,P是△ABC所在平面内一点,且满足PA⊥PB,则PC的取值范围为$\sqrt{5}$-1≤PC≤$\sqrt{5}$+1.
如图,在等腰直角三角形ABC中,∠ABC=90°,AB=BC=2,P是△ABC所在平面内一点,且满足PA⊥PB,则PC的取值范围为$\sqrt{5}$-1≤PC≤$\sqrt{5}$+1.