题目内容
20.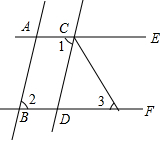 如图,已知AB∥CD,∠1=∠2,CF平分∠DCE.
如图,已知AB∥CD,∠1=∠2,CF平分∠DCE.(1)试判断直线AC与BD有怎样的位置关系?并说明理由;
(2)若∠1=80°,求∠3的度数.
分析 (1)先根据AB∥CD得出∠2=∠CDF,再由∠1=∠2即可得出结论;
(2)先求出∠ECD的度数,再由角平分线的性质求出∠ECF的度数,根据平行线的性质即可得出结论.
解答 解:(1)AC∥BD.
理由:∵AB∥CD,
∴∠2=∠CDF.
∵∠1=∠2,
∴∠1=∠CDF,
∴AC∥BD;
(2)∵∠1=80°,
∴∠ECD=180°-∠1=180°-80°=100°.
∵CF平分∠ECD,
∴∠ECF=$\frac{1}{2}$∠ECD=$\frac{1}{2}$×100°=50°.
∵AC∥BD,
∴∠3=∠ECF=50°.
点评 本题考查的是平行线的判定与性质,熟知平行线的判定定理是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.下列事件中,是确定事件的是( )
| A. | 明天太阳从东方升起 | B. | 打开电视机正在播放动画片 | ||
| C. | 篮球运动员身高都在2米以上 | D. | 抛一枚硬币,正面向上 |
15. 如图,在三角形纸片ABC中,∠B=∠C=35°,过边BC上的一点,沿与BC垂直的方向将它剪开,分成三角形和四边形两部分,则在四边形中,最大的内角的度数为( )
如图,在三角形纸片ABC中,∠B=∠C=35°,过边BC上的一点,沿与BC垂直的方向将它剪开,分成三角形和四边形两部分,则在四边形中,最大的内角的度数为( )
 如图,在三角形纸片ABC中,∠B=∠C=35°,过边BC上的一点,沿与BC垂直的方向将它剪开,分成三角形和四边形两部分,则在四边形中,最大的内角的度数为( )
如图,在三角形纸片ABC中,∠B=∠C=35°,过边BC上的一点,沿与BC垂直的方向将它剪开,分成三角形和四边形两部分,则在四边形中,最大的内角的度数为( )| A. | 110° | B. | 115° | C. | 120° | D. | 125° |
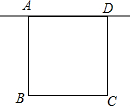 如图,在矩形ABCD中,AB=3,点P是直线AD上一点,若满足△PBC是等腰三角形的点P有且只有3个,则AD的长为3或2$\sqrt{3}$.
如图,在矩形ABCD中,AB=3,点P是直线AD上一点,若满足△PBC是等腰三角形的点P有且只有3个,则AD的长为3或2$\sqrt{3}$.