题目内容
14.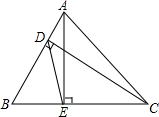 在△ABC中,CD,AE分别为AB、BC边上的高,∠B=60°,求证:DE=$\frac{1}{2}$AC.
在△ABC中,CD,AE分别为AB、BC边上的高,∠B=60°,求证:DE=$\frac{1}{2}$AC.
分析 根据直角三角形的性质,可得BE与AB,BD与BC的关系,根据两边对应成比例且夹角相等的两个三角形,可得△BDE与△BAC的关系,根据相似三角形的性质,可得答案.
解答 证明:∵AE⊥BC,CD⊥AB,
∴∠AEB=∠BDC=90°.
∵∠ABC=60°,
∴∠BAE=30°,
∴AB=2BE,
即$\frac{BE}{AB}$=$\frac{1}{2}$;
∴∠BCD=30°,
∴BC=2BD,
即$\frac{BD}{BC}$=$\frac{1}{2}$.
∵∠B=∠B,
∴△BDE∽△BAC,
∴$\frac{DE}{AC}$=$\frac{BD}{BC}$,
∴DE=$\frac{1}{2}$AC.
点评 本题考查了相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解题的关键.

练习册系列答案
相关题目
6.-$\frac{1}{2}$的相反数是( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -2 | D. | -$\frac{1}{2}$ |
3.某公司股票上周五收盘价是每股26.5元,下表为本星期内每日该股票的涨跌情况:
(1)星期四收盘时,每股是31.5元?
(2)本周内该股票的最高价是每股35元?最低价是每股25.5元?
(3)与上周五相比,本周五收盘时价格是升了,还是降了?请说明理由.
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 (单位:元) | +4 | +4.5 | -1 | -2.5 | -6 |
(2)本周内该股票的最高价是每股35元?最低价是每股25.5元?
(3)与上周五相比,本周五收盘时价格是升了,还是降了?请说明理由.
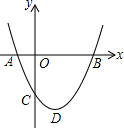 如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1,3.与y轴负半轴交于点C,在下面五个结论中:
如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1,3.与y轴负半轴交于点C,在下面五个结论中: 如图,已知△ABC中,CF⊥AB于F,BE⊥AC于F,若S△ABC=36cm2,S△AEF=4cm2,求sinA的值.
如图,已知△ABC中,CF⊥AB于F,BE⊥AC于F,若S△ABC=36cm2,S△AEF=4cm2,求sinA的值. 在Rt△ABC中,∠ABC=90°,AC=6,P、Q分别为AC、BC的中点,AQ、BP相交于点O,则OP=1.
在Rt△ABC中,∠ABC=90°,AC=6,P、Q分别为AC、BC的中点,AQ、BP相交于点O,则OP=1.