题目内容
4. 在Rt△ABC中,∠ABC=90°,AC=6,P、Q分别为AC、BC的中点,AQ、BP相交于点O,则OP=1.
在Rt△ABC中,∠ABC=90°,AC=6,P、Q分别为AC、BC的中点,AQ、BP相交于点O,则OP=1.
分析 先根据直角三角形斜边上的中线等于斜边的一半求出BP=$\frac{1}{2}$AC=3,再由P、Q分别为AC、BC的中点,AQ、BP相交于点O,得出O为△ABC的重心,然后根据重心的性质得出OP=$\frac{1}{3}$BP=1.
解答 解:∵在Rt△ABC中,∠ABC=90°,AC=6,P为AC的中点,
∴BP=$\frac{1}{2}$AC=3.
∵P、Q分别为AC、BC的中点,AQ、BP相交于点O,
∴O为△ABC的重心,
∴OB=2OP,
∵OP+OB=BP,
∴OP=$\frac{1}{3}$BP=1.
故答案为1.
点评 本题考查了三角形的重心的定义及性质,三角形三边中线的交点叫做三角形的重心,重心到顶点的距离与重心到对边中点的距离之比为2:1.同时考查了直角三角形斜边上的中线的性质.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
13.抛物线y=(x-2)2+3的顶点是( )
| A. | (2,-3) | B. | (1,4) | C. | (3,4) | D. | (2,3) |
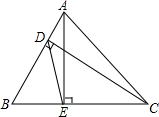 在△ABC中,CD,AE分别为AB、BC边上的高,∠B=60°,求证:DE=$\frac{1}{2}$AC.
在△ABC中,CD,AE分别为AB、BC边上的高,∠B=60°,求证:DE=$\frac{1}{2}$AC.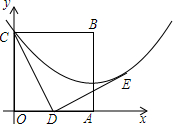 边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点 E在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点.
边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点 E在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点. 在△ABC中,用直尺和圆规作出∠B的平分线(不写作法,保留作图痕迹).
在△ABC中,用直尺和圆规作出∠B的平分线(不写作法,保留作图痕迹).