题目内容
19.在梯形ABCD中,AB∥CD,AB=1,CD=2,EF∥AB,且AF:FD=1:2013,则EF=$\frac{2015}{2014}$.分析 连接AC交EF于O,根据平行线分线段成比例得到$\frac{BE}{CE}=\frac{AF}{DF}$=$\frac{1}{2013}$,于是得到$\frac{AF}{AD}=\frac{1}{2014}$,$\frac{CE}{BC}=\frac{2013}{2014}$,通过△AFO∽△ADC,△CEO∽△CBA,由相似三角形的性质得到$\frac{OF}{CD}=\frac{AF}{AD}$,$\frac{OE}{AB}=\frac{CE}{BC}$,代入数据即可得到结论.
解答  解:如图,连接AC交EF于O,
解:如图,连接AC交EF于O,
∵AB∥CD,EF∥AB,
∴EF∥AB∥CD,
∴$\frac{BE}{CE}=\frac{AF}{DF}$=$\frac{1}{2013}$,
∴$\frac{AF}{AD}=\frac{1}{2014}$,$\frac{CE}{BC}=\frac{2013}{2014}$,
∵EF∥AB∥CD,
∴△AFO∽△ADC,△CEO∽△CBA,
∴$\frac{OF}{CD}=\frac{AF}{AD}$,$\frac{OE}{AB}=\frac{CE}{BC}$,
∴$\frac{OF}{2}=\frac{1}{2014}$,$\frac{OE}{1}=\frac{2013}{2014}$,
∴OF=$\frac{2}{2014}$,OE=$\frac{2013}{2014}$,
∴EF=OF+OE=$\frac{2015}{2014}$.
故答案为:$\frac{2015}{2014}$.
点评 本题考查了相似三角形的判定和性质,梯形的性质,平行线分线段成比例定理.熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
4.-$\frac{4}{5}$的倒数是( )
| A. | $\frac{5}{4}$ | B. | -$\frac{5}{4}$ | C. | $\frac{4}{5}$ | D. | -$\frac{4}{5}$ |
11.某中学体育节有八字绳项目,其中5个班比赛记录如下(以跳200个为基准,超过的个数记为正数,不足的个数记为负数);
(1)七(3)班比七(2)班多跳了多少个?
(2)七年级5个班平均每班八字绳跳了多少个?
| 班级 | 七(1)班 | 七(2)班 | 七(3)班 | 七(4)班 | 七(5)班 |
| 超出或不足 | 0 | -20 | +65 | +80 | -75 |
(2)七年级5个班平均每班八字绳跳了多少个?
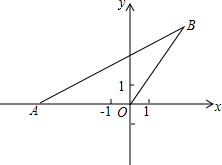 已知二次函数y=ax2+bx的图象经过点A(-5,0)和点B,其中点B在第一象限,且OA=OB,tan∠BAO=$\frac{1}{2}$
已知二次函数y=ax2+bx的图象经过点A(-5,0)和点B,其中点B在第一象限,且OA=OB,tan∠BAO=$\frac{1}{2}$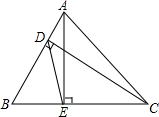 在△ABC中,CD,AE分别为AB、BC边上的高,∠B=60°,求证:DE=$\frac{1}{2}$AC.
在△ABC中,CD,AE分别为AB、BC边上的高,∠B=60°,求证:DE=$\frac{1}{2}$AC.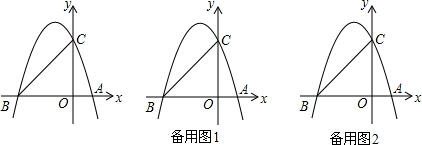
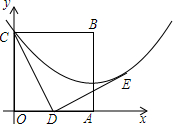 边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点 E在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点.
边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点 E在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点.