题目内容
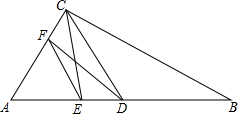 如图,在△ABC中,中线CD⊥AC,CD=AC,点E在AB上,且AE=
如图,在△ABC中,中线CD⊥AC,CD=AC,点E在AB上,且AE=| 1 |
| 2 |
(1)△EDF与△DCB相似吗?为什么?(提示:设AE=a)
(2)判断∠CDF与∠B是否相等,并说明理由.
考点:相似三角形的判定
专题:常规题型
分析:(1)设AE=a,则BE=2a,则AB=3a,可计算出AD=BD=
a,DE=AD-AE=
a,由CD⊥AC,CD=AC得到△ACD为等腰直角三角形,所以CD=
AD=
a;根据EF∥CD得到∠DEF=∠BDC,△AEF∽△ADC,再利用相似的性质得
=
,可表示出EF=
a,由于
=
=
,且∠DEF=∠CDB,于是根据三角形相似的判定即可得到△DEF∽△CDB;
(2)先由△DEF∽△CDB得到∠DFE=∠B,再利用EF∥CD得到∠DFE=∠CDF,所以∠CDF=∠B.
| 3 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
3
| ||
| 4 |
| EF |
| CD |
| AE |
| AD |
| ||
| 2 |
| EF |
| BD |
| DE |
| CD |
| ||
| 3 |
(2)先由△DEF∽△CDB得到∠DFE=∠B,再利用EF∥CD得到∠DFE=∠CDF,所以∠CDF=∠B.
解答:解:(1)△EDF与△DCB相似.理由如下:
设AE=a,则BE=2a,
∴AB=3a,
∵D为AB的中点,
∴AD=BD=
a,
∴DE=AD-AE=
a,
∵CD⊥AC,CD=AC,
∴△ACD为等腰直角三角形,
∴CD=
AD=
a,
∵EF∥CD,
∴∠DEF=∠BDC,
∴△AEF∽△ADC,
∴
=
,即
=
,解得EF=
a,
∵
=
=
,
=
=
,
∴
=
,
而∠DEF=∠CDB,
∴△DEF∽△CDB;
(2)∠CDF与∠B相等.理由如下:
∵△DEF∽△CDB,
∴∠DFE=∠B,
∵EF∥CD,
∴∠DFE=∠CDF,
∴∠CDF=∠B.
设AE=a,则BE=2a,
∴AB=3a,
∵D为AB的中点,
∴AD=BD=
| 3 |
| 2 |
∴DE=AD-AE=
| 1 |
| 2 |
∵CD⊥AC,CD=AC,
∴△ACD为等腰直角三角形,
∴CD=
| ||
| 2 |
3
| ||
| 4 |
∵EF∥CD,
∴∠DEF=∠BDC,
∴△AEF∽△ADC,
∴
| EF |
| CD |
| AE |
| AD |
| EF | ||||
|
| a | ||
|
| ||
| 2 |
∵
| EF |
| BD |
| ||||
|
| ||
| 3 |
| DE |
| CD |
| ||||
|
| ||
| 3 |
∴
| EF |
| BD |
| DE |
| CD |
而∠DEF=∠CDB,
∴△DEF∽△CDB;
(2)∠CDF与∠B相等.理由如下:
∵△DEF∽△CDB,
∴∠DFE=∠B,
∵EF∥CD,
∴∠DFE=∠CDF,
∴∠CDF=∠B.
点评:本题考查了三角形相似的判定:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;两组对应边的比相等且夹角对应相等的两个三角形相似.也考查了相似的性质和平行线的性质.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
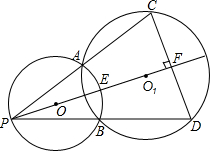 如图所示,已知⊙O与⊙O1相交于A、B两点,P为⊙O上的一点,PA、PB的延长线分别交⊙O1于C、D两点,PF⊥CD于F,PF交⊙O于E,求证:PE是⊙O的直径.
如图所示,已知⊙O与⊙O1相交于A、B两点,P为⊙O上的一点,PA、PB的延长线分别交⊙O1于C、D两点,PF⊥CD于F,PF交⊙O于E,求证:PE是⊙O的直径.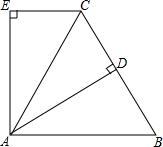 已知:如图,△ABC是等边三角形,AD⊥BC于D,CE∥AB,且AE⊥EC,求证:AE=AD.
已知:如图,△ABC是等边三角形,AD⊥BC于D,CE∥AB,且AE⊥EC,求证:AE=AD. 用8块相同的长方形地砖拼成一块长方形地面,地面周长为150厘米地砖的拼放方式如图所示,地面的宽是多少米?
用8块相同的长方形地砖拼成一块长方形地面,地面周长为150厘米地砖的拼放方式如图所示,地面的宽是多少米?