题目内容
圆锥的底面积为4π,高为4
,求圆锥的侧面展开图的圆心角的度数.
| 2 |
考点:圆锥的计算
专题:
分析:圆锥的底面周长等于圆锥的侧面展开图的弧长,首先求得展开图的弧长,然后根据弧长公式即可求解.
解答:解:∵圆锥的底面积为4π,
∴圆锥的底面半径为2,
∴圆锥侧面展开图的弧长是:4π,
∵高为4
,
∴圆锥的母线长为
=6,
设圆心角的度数是x度.则
=4π,
解得:x=120.
∴圆锥的侧面展开图的圆心角的度数为120°.
∴圆锥的底面半径为2,
∴圆锥侧面展开图的弧长是:4π,
∵高为4
| 2 |
∴圆锥的母线长为
22+(4
|
设圆心角的度数是x度.则
| xπ×6 |
| 180 |
解得:x=120.
∴圆锥的侧面展开图的圆心角的度数为120°.
点评:本题考查了圆锥的计算,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
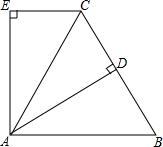 已知:如图,△ABC是等边三角形,AD⊥BC于D,CE∥AB,且AE⊥EC,求证:AE=AD.
已知:如图,△ABC是等边三角形,AD⊥BC于D,CE∥AB,且AE⊥EC,求证:AE=AD. 如图,AC⊥CD于点C,∠1与∠2互余,判断AB、CD是否平行,并说明理由.
如图,AC⊥CD于点C,∠1与∠2互余,判断AB、CD是否平行,并说明理由. 用8块相同的长方形地砖拼成一块长方形地面,地面周长为150厘米地砖的拼放方式如图所示,地面的宽是多少米?
用8块相同的长方形地砖拼成一块长方形地面,地面周长为150厘米地砖的拼放方式如图所示,地面的宽是多少米?