题目内容
以下说法中：
①五边形的内角和是540°；
②n边形的对角线有
条；
③同旁内角互补；
④三角形的三个内角中至少有2个角是锐角．
真命题的个数是（ ）
①五边形的内角和是540°；
②n边形的对角线有
| n(n-2) |
| 2 |
③同旁内角互补；
④三角形的三个内角中至少有2个角是锐角．
真命题的个数是（ ）
| A、0 | B、1 | C、2 | D、3 |
考点：命题与定理
专题：
分析：根据多边的内角和公式对①进行判断；根据n边形的对角线公式对②进行判断；根据平行线的性质对③进行判断；根据三角形内角和定理对④进行判断．
解答：解：五边形的内角和是540°，所以①为真命题；
n边形的对角线有
n（n-3）条，所以②为假命题；
两直线平行，同旁内角互补，所以③为假命题；
三角形的三个内角中至少有2个角是锐角，所以④为真命题．
故选C．
n边形的对角线有
| 1 |
| 2 |
两直线平行，同旁内角互补，所以③为假命题；
三角形的三个内角中至少有2个角是锐角，所以④为真命题．
故选C．
点评：本题考查了命题与定理：判断事物的语句叫命题；正确的命题称为真命题，错误的命题称为假命题；经过推理论证的真命题称为定理．
练习册系列答案
相关题目
若方程组
与
有相同的解，则a、b的值为（ ）
|
|
| A、2，3 | B、3，2 |
| C、2，-1 | D、-1，2 |
下列说法：
①不等式-3x＞9的解集是x＞-3；
②不等式x＜10的整数解有无数个；
③不等式x＜2的正整数解只有一个；
④-1是不等式2x-1＜0的一个解．
其中正确的个数为（ ）
①不等式-3x＞9的解集是x＞-3；
②不等式x＜10的整数解有无数个；
③不等式x＜2的正整数解只有一个；
④-1是不等式2x-1＜0的一个解．
其中正确的个数为（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
有理数a、b在数轴上的对应点如图所示，则下面式子中正确的是（ ）①b＜0＜a； ②|-b|＞|-a|； ③ab＞0； ④a-b＜a+b．
| A、①② | B、①④ | C、②③ | D、③④ |
已知x=2是一元二次方程x2+mx-8=0的一个解，则m的值是（ ）
| A、2 | B、-2 | C、-4 | D、2或-4 |
下列各组数中不能作为直角三角形三边长的是（ ）
| A、1.5，2，2.5 |
| B、7，24，25 |
| C、6，8，10 |
| D、8，12，15 |
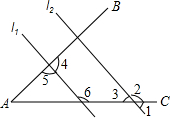如图，直线l1，l2分别截射线AB，AC，若l1∥l2，则下列各角度数关系正确的是（ ）| A、∠5+∠1=180° |
| B、∠4+∠2＞180° |
| C、∠6+∠3＜180° |
| D、∠4+∠6＜180° |
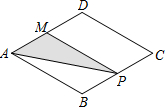如图，菱形ABCD中，AB=2，∠B=120°，点M是AD的中点，点P由点A出发，沿A→B→C→D作匀速运动，到达点D停止，则△APM的面积y与点P经过的路程x之间的函数关系的图象大致是（ ）
