题目内容
9.已知:$\sqrt{4-2\sqrt{3}}$x=2tan45°+|1-2$\sqrt{3}$|-4cos30°+($\frac{2009}{π-3}$)0.求代数式($\frac{x-1}{x-3}$-$\frac{x+3}{x}$)÷$\frac{{x}^{2}-8x-9}{{x}^{2}+x}$的值.分析 先将代数式化简,然后解出关于x的方程,最后将x的值代入即可得出答案.
解答 解:原式=[$\frac{x(x-1)}{x(x-3)}$-$\frac{(x-3)(x+3)}{x(x-3)}$]÷$\frac{(x-9)(x+1)}{x(x+1)}$
=$\frac{-x+9}{x(x-3)}$×$\frac{x}{x-9}$
=$\frac{-1}{x-3}$,
∵$\sqrt{4-2\sqrt{3}}$x=2tan45°+|1-2$\sqrt{3}$|-4cos30°+($\frac{2009}{π-3}$)0,
∴$\sqrt{(\sqrt{3}-1)^{2}}$x=2×1+2$\sqrt{3}$-1-4×$\frac{\sqrt{3}}{2}$+1
∴($\sqrt{3}$-1)x=2,
∴x=$\sqrt{3}$+1,
∴把x=$\sqrt{3}$+1代入$\frac{-1}{x-3}$,
∴原式=$\frac{-1}{\sqrt{3}+1-3}$=$\sqrt{3}$+2
点评 本题考查分式的化简,涉及分式的基本性质,实数运算,一元一次方程等知识,综合程度较高.

练习册系列答案
相关题目
19.在式子$\frac{1}{x-1}$,$\frac{1}{x-2}$,$\sqrt{x-1}$,$\sqrt{x-2}$中,x可以取1和2的是( )
| A. | $\frac{1}{x-1}$ | B. | $\frac{1}{x-2}$ | C. | $\sqrt{x-1}$ | D. | $\sqrt{x-2}$ |
20. 如图,在平面直角坐标系中,点P(-1,2)向右平移3个单位长度后的坐标是( )
如图,在平面直角坐标系中,点P(-1,2)向右平移3个单位长度后的坐标是( )
 如图,在平面直角坐标系中,点P(-1,2)向右平移3个单位长度后的坐标是( )
如图,在平面直角坐标系中,点P(-1,2)向右平移3个单位长度后的坐标是( )| A. | (2,2) | B. | (-4,2) | C. | (-1,5) | D. | (-1,-1) |

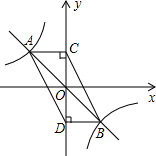 如图,函数y=-x与函数y=-$\frac{4}{x}$的图象相交于A、B两点,过A、B两点分别作y轴的垂线,垂足分别为点C、D,则四边形ACBD的面积为( )
如图,函数y=-x与函数y=-$\frac{4}{x}$的图象相交于A、B两点,过A、B两点分别作y轴的垂线,垂足分别为点C、D,则四边形ACBD的面积为( )