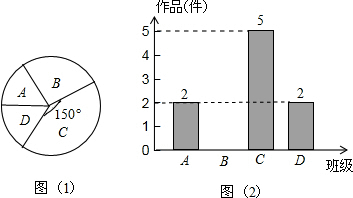
题目内容
14.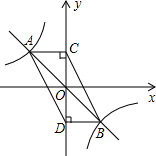 如图,函数y=-x与函数y=-$\frac{4}{x}$的图象相交于A、B两点,过A、B两点分别作y轴的垂线,垂足分别为点C、D,则四边形ACBD的面积为( )
如图,函数y=-x与函数y=-$\frac{4}{x}$的图象相交于A、B两点,过A、B两点分别作y轴的垂线,垂足分别为点C、D,则四边形ACBD的面积为( )| A. | 8 | B. | 6 | C. | 4 | D. | 2 |
分析 反比例函数y=xk图象中任取一点,向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{1}{2}$|k|,据此进行计算即可.
解答 解:∵过A、B两点分别作y轴的垂线,垂足分别为点C、D,
∴△AOC的面积=$\frac{1}{2}$×|-4|=2,
又∵AO=BO,∠AOC=∠BOD,
∴△AOC≌△BOD,
∴CO=DO,
∴四边形ADBC是平行四边形,
∴四边形ACBD的面积=4×△AOC的面积=4×2=8,
故选(A).
点评 本题主要考查了反比例函数中k的几何意义以及平行四边形的判定与性质,在反比例函数的图象上任意一点向一条坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{1}{2}$|k|,且保持不变.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
19.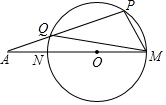 如图,MN是⊙O的直径,∠A=20°,∠PMQ=50°,以PM为边作圆的内接正多边形,则这个正多边形是( )
如图,MN是⊙O的直径,∠A=20°,∠PMQ=50°,以PM为边作圆的内接正多边形,则这个正多边形是( )
 如图,MN是⊙O的直径,∠A=20°,∠PMQ=50°,以PM为边作圆的内接正多边形,则这个正多边形是( )
如图,MN是⊙O的直径,∠A=20°,∠PMQ=50°,以PM为边作圆的内接正多边形,则这个正多边形是( )| A. | 正七边形 | B. | 正八边形 | C. | 正六边形 | D. | 正十边形 |
 如图,矩形ABCD位于二次函数y=-2x2+4x与x轴所围区域内,BC边在x轴上,A,D两点位于二次函数图象上,则矩形ABCD周长的最大值为( )
如图,矩形ABCD位于二次函数y=-2x2+4x与x轴所围区域内,BC边在x轴上,A,D两点位于二次函数图象上,则矩形ABCD周长的最大值为( )