题目内容
17.已知:在△ABC中,∠ABC=90°,AB=BC;在△ADE中,∠ADE=90°,AD=DE.连接EC,取EC的中点M,连接DM和BM.(1)若点D在边AC上,点E在边AB上且与点B不重合,如图(1).求证:BM=DM,且BM⊥DM;
(2)如果将图(1)中的△ADE绕点A逆时针方向旋转45°的角,请画出图形.(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立请举出反例.

分析 (1)利用直角三角形斜边上的中线等于斜边的一半得出BM=DM=$\frac{1}{2}$EC,再利用∠1=∠2,∠3=∠4,∠BMD=2(∠1+∠3),即可得出答案;
(2)首先证明△EMD≌△CMN,得CN=AD,DM=MN,再由AB=AC,可得BD=BN,从而可得△DBN是等腰直角三角形,且BM是底边DN上的中线,再利用等腰三角形的三线合一的性质和直角三角形的性质即可得到△BMD为等腰直角三角形;
解答 解:(1)△BMD是等腰三角形,
理由是:∵∠ABC=∠ADE=90°,
∴∠EDC=90°,
∵点M是CE的中点,
∴BM=$\frac{1}{2}$CE,DM=$\frac{1}{2}$CE,
∴BM=DM,
∴∠1=∠2,∠3=∠4,
∵∠BME=∠1+∠2,∠EMD=∠3+∠4,
∴∠BMD=2(∠1+∠3),
∵△ABC等腰直角三角形,
∴∠BCA=45°,
∴∠BMD=90°,
∴BM=DM且BM⊥DM;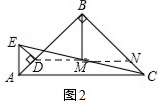
故答案为:BM=DM且BM⊥DM.
(2)结论:BM=DM,BM⊥DM,
证明:∵∠ABC=∠ADE=90°,
∴ED∥BC,
∴∠DEM=∠MCB,
在△EMD和△CMN中,
$\left\{\begin{array}{l}{∠DEM=∠NCM}\\{EM=CM}\\{∠EMD=∠NMC}\end{array}\right.$,
∴△EMD≌△CMN(ASA),
∴CN=AD,DM=MN,
∵BA=BC,
∴BD=BN,
∴△DBN是等腰直角三角形,且BM是底边的中线,
∴BM⊥DM,BM=$\frac{1}{2}$DN=DM,
∴△BMD为等腰直角三角形,
∴BM⊥DM,BM=DM.
点评 本题考查了等腰直角三角形的性质,全等三角形的性质和判定,直角三角形的性质的应用,解题的关键是学会添加辅助线构造全等三角形,属于中考常考题型.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案 如图,在Rt△ABO中,斜边AB=1,若OC∥BA,∠AOC=36°,则( )
如图,在Rt△ABO中,斜边AB=1,若OC∥BA,∠AOC=36°,则( )| A. | 点B到AO的距离为sin54° | B. | 点A到OC的距离为sin36°sin54° | ||
| C. | 点B到AO的距离为tan36° | D. | 点A到OC的距离为cos36°sin54° |
 如图,已知五边形A'B'C'D'E'是五边形ABCDE的位似图形,但被小伟擦去了一部分,请你将它补完整.
如图,已知五边形A'B'C'D'E'是五边形ABCDE的位似图形,但被小伟擦去了一部分,请你将它补完整.
 如图,AB是半径为1的半圆O的直径,弦CD∥AB,且$\widehat{CD}$为90°,求图中阴影部分的面积.
如图,AB是半径为1的半圆O的直径,弦CD∥AB,且$\widehat{CD}$为90°,求图中阴影部分的面积.