题目内容
对于任意正整数n,能整除(3n+1)(3n-1)-(3-n)(3+n)的整数是 .
考点:平方差公式
专题:
分析:根据平方差公式,可化简整式,根据提取公因式,可得因数.
解答:解:(3n+1)(3n-1)-(3-n)(3+n)=9n2-1-(9-n2)
=10n2-10
=10(n2-1),
10能整除(3n+1)(3n-1)-(3-n)(3+n),
故答案为:10.
=10n2-10
=10(n2-1),
10能整除(3n+1)(3n-1)-(3-n)(3+n),
故答案为:10.
点评:本题考查了平方差公式,利用了平方差公式,提公因式分解因式.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
分式-
可化简为( )
| a+b |
| (a-b)(a+b) |
| A、0 | ||
B、
| ||
C、
| ||
D、
|
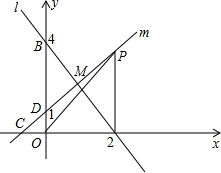 如图,直线l:y=4-2x与x轴、y轴分别交于点A、B,且与直线m相交于点M(1,2),已知直线m经过点C(-1,0),且与y轴交于点D.
如图,直线l:y=4-2x与x轴、y轴分别交于点A、B,且与直线m相交于点M(1,2),已知直线m经过点C(-1,0),且与y轴交于点D. 如图所示,已知直线y=-
如图所示,已知直线y=-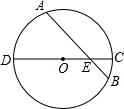 如图,CD为⊙O的直径,弦AB交CD于点E,∠CEB=45°,DE=9cm,CE=3cm,求弦AB的长.
如图,CD为⊙O的直径,弦AB交CD于点E,∠CEB=45°,DE=9cm,CE=3cm,求弦AB的长.