题目内容
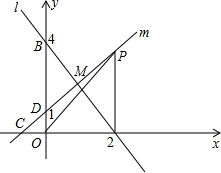 如图,直线l:y=4-2x与x轴、y轴分别交于点A、B,且与直线m相交于点M(1,2),已知直线m经过点C(-1,0),且与y轴交于点D.
如图,直线l:y=4-2x与x轴、y轴分别交于点A、B,且与直线m相交于点M(1,2),已知直线m经过点C(-1,0),且与y轴交于点D.(1)求点A、B的坐标以及直线m的解析式;
(2)求四边形OAMD的面积;
(3)若P是直线m上一动点,试求OP+AP的最小值;
(4)若点N在x轴上,且△OMN是等腰三角形,请直接写出所有满足条件的点N的坐标.
考点:一次函数综合题
专题:
分析:(1)在解析式y=4-2x中令x=0,求得y的值即可求得与y轴的交点坐标,令y=0,求得x的值,即可得到与x轴的交点的坐标,利用待定系数法求得直线m的解析式;
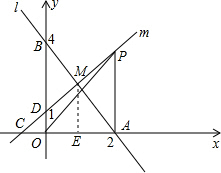
(2)首先求得M的坐标,作MN⊥x轴于点E,根据四边形OAMD的面积=S△AME+S梯形DOEM即可求解;
(3)首先求得O关于直线m的对称点的坐标,则此点与A之间的线段的长度就是所求的OP+AP的最小值;
(4)分O是顶角顶点,M是顶角顶点,N是顶角顶点三种情况进行讨论,根据等腰三角形的定义即可求解.
(2)首先求得M的坐标,作MN⊥x轴于点E,根据四边形OAMD的面积=S△AME+S梯形DOEM即可求解;
(3)首先求得O关于直线m的对称点的坐标,则此点与A之间的线段的长度就是所求的OP+AP的最小值;
(4)分O是顶角顶点,M是顶角顶点,N是顶角顶点三种情况进行讨论,根据等腰三角形的定义即可求解.
解答:解:(1)在y=4-2x中,令x=0,解得:y=4,则B的坐标是(0,4),
令y=0,则4-2x=0,解得:x=2,则A的坐标是(2,0).
设直线m的解析式是y=kx+b,
则
,
解得:
.
则直线m的方程是y=x+1;
(2)解方程组
,
解得:
,
则M的坐标是(1,2),
作MN⊥x轴于点E,则E的坐标是(1,0),则ME=2,AE=2-1=1.
则S△AME=
×1×2=1,S梯形DOEM=
(1+2)×1=
,
则S四边形OAMD=1+
=
;
(3)经过O且与直线m垂直的直线的解析式是:y=-x,
根据题意得:
,
解得:
,
则直线y=-x和直线m的交点坐标是(-
,
),设O关于直线m的对称点的坐标是(m,n),
则
,
解得:
,即O关于直线m的对称点坐标是(-1,1).
则OP+AP最小值是:
=
;
(4)OM=
=
,
当O是顶角顶点时,N的坐标是(-
,0)或(
,0);
当M是顶角顶点时,ME是O和N的对称轴,则N的坐标是(2,0);
当N是顶角顶点时,OM的中点坐标是(
,1),设直线OM的解析式是y=ax,则把(1,2)代入解析式得:a=2,即解析式是y=2x,
则经过OM的中点,且与OM垂直的直线的解析式是y=-
x+b,则-
×
+b=1,
解得:b=
,则直线的解析式是:y=-
x+
,令y=0,解得:x=
,则N的坐标是(
,0).
总之,N的坐标是:(-
,0)或(
,0)或(2,0)或(
,0).
令y=0,则4-2x=0,解得:x=2,则A的坐标是(2,0).
设直线m的解析式是y=kx+b,
则
|
解得:
|
则直线m的方程是y=x+1;
(2)解方程组
|
解得:
|
则M的坐标是(1,2),
作MN⊥x轴于点E,则E的坐标是(1,0),则ME=2,AE=2-1=1.
则S△AME=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
则S四边形OAMD=1+
| 3 |
| 2 |
| 5 |
| 2 |
(3)经过O且与直线m垂直的直线的解析式是:y=-x,
根据题意得:
|
解得:
|

则直线y=-x和直线m的交点坐标是(-
| 1 |
| 2 |
| 1 |
| 2 |
则
|
解得:
|
则OP+AP最小值是:
| (2+1)2+12 |
| 10 |
(4)OM=
| 12+22 |
| 5 |
当O是顶角顶点时,N的坐标是(-
| 10 |
| 10 |
当M是顶角顶点时,ME是O和N的对称轴,则N的坐标是(2,0);
当N是顶角顶点时,OM的中点坐标是(
| 1 |
| 2 |
则经过OM的中点,且与OM垂直的直线的解析式是y=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得:b=
| 5 |
| 4 |
| 1 |
| 2 |
| 5 |
| 4 |
| 5 |
| 2 |
| 5 |
| 2 |
总之,N的坐标是:(-
| 10 |
| 10 |
| 5 |
| 2 |
点评:本题是一次函数与等腰三角形的综合题,主要考查了待定系数法求函数的解析式,以及等腰三角形的计算,正确进行讨论是关键.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
甲乙两超市为了促销一种定价相同的商品,甲超市连续两次降价5%,乙超市一次性降价10%,在哪个超市购买这种商品合算?下列选项中正确的是( )
| A、甲超市 |
| B、乙超市 |
| C、两个超市一样 |
| D、与商品的价格有关 |