题目内容
11.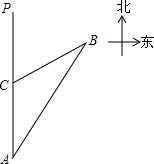 一船以每小时36海里的速度向正北航行到A处,发现它的北偏东30°方向上有一灯塔B,船继续向北航行40分钟后到达C处,发现灯塔B在北偏东60°方向上,求此船与灯塔的距离.
一船以每小时36海里的速度向正北航行到A处,发现它的北偏东30°方向上有一灯塔B,船继续向北航行40分钟后到达C处,发现灯塔B在北偏东60°方向上,求此船与灯塔的距离.
分析 对照图形理解方向角知:∠A=30°,∠PCB=60°,根据三角形外角的性质得出∠B=30°,利用等角对等边得到BC=AC=24海里.
解答 解:∵∠PCB=∠A+∠B=60°,∠A=30°,
∴∠B=30°,
∴∠A=∠B=30°,
∴BC=AC.
∵AC=36×$\frac{40}{60}$=24,
∴BC=AC=24(海里).
即此船与灯塔的距离是24海里.
点评 本题考查了解直角三角形的应用-方向角问题,三角形外角的性质,等腰三角形的判定,正确理解方向角的定义是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
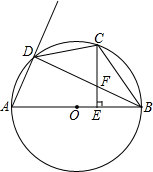 如图,AB是⊙O的直径,C是弧BD的中点,CE⊥AB,垂足为E,BD交CE于点F.
如图,AB是⊙O的直径,C是弧BD的中点,CE⊥AB,垂足为E,BD交CE于点F.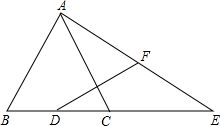 如图,已知在△ABC中,AB=AC=2$\sqrt{5}$,sin∠B=$\frac{2\sqrt{5}}{5}$,D为边BC的中点,E为边BC的延长线上一点,且CE=BC.联结AE,F为线段AE的中点.
如图,已知在△ABC中,AB=AC=2$\sqrt{5}$,sin∠B=$\frac{2\sqrt{5}}{5}$,D为边BC的中点,E为边BC的延长线上一点,且CE=BC.联结AE,F为线段AE的中点.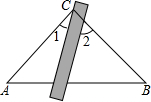 如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上,若∠2=65°,则∠1的度数等于25°.
如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上,若∠2=65°,则∠1的度数等于25°.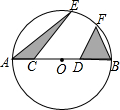 如图,⊙O的半径为6,AB是⊙O的直径,C、D是AB的三等分点,∠ECB=∠FDB=60°,则图中阴影部分的面积是6$\sqrt{11}$.
如图,⊙O的半径为6,AB是⊙O的直径,C、D是AB的三等分点,∠ECB=∠FDB=60°,则图中阴影部分的面积是6$\sqrt{11}$.