题目内容
10.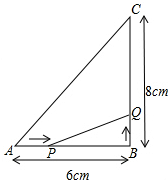 如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.
如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.(1)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,经过几秒,使△PBQ的面积等于8cm2?
(2)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
(3)若P点沿射线AB方向从A点出发以1cm/s的速度移动,点Q沿射线CB方向从C点出发以2cm/s的速度移动,P,Q同时出发,问几秒后,△PBQ的面积为1?
分析 (1)设经过x秒,使△PBQ的面积等于8cm2,根据等量关系:△PBQ的面积等于8cm2,列出方程求解即可;
(2)设经过y秒,线段PQ能否将△ABC分成面积相等的两部分,根据面积之间的等量关系和判别式即可求解;
(3)分三种情况:①点P在线段AB上,点Q在线段CB上(0<x<4);②点P在线段AB上,点Q在线段CB上(4<x<6);③点P在射线AB上,点Q在射线CB上(x>6);进行讨论即可求解.
解答 解:(1)设经过x秒,使△PBQ的面积等于8cm2,依题意有
$\frac{1}{2}$(6-x)•2x=8,
解得x1=2,x2=4,
经检验,x1,x2均符合题意.
故经过2秒或4秒,△PBQ的面积等于8cm2;
(2)设经过y秒,线段PQ能否将△ABC分成面积相等的两部分,依题意有
△ABC的面积=$\frac{1}{2}$×6×8=24,
$\frac{1}{2}$(6-y)•2y=24,
y2-6y+24=0,
∵△=b2-4ac=36-4×24=-60<0,
∴此方程无实数根,
∴线段PQ不能否将△ABC分成面积相等的两部分;
(3)①点P在线段AB上,点Q在线段CB上(0<x<4),
设经过m秒,依题意有
$\frac{1}{2}$(6-m)(8-2x)=1,
m2-10m+23=0,
解得m1=5+$\sqrt{2}$,m2=5-$\sqrt{2}$,
经检验,m1=5+$\sqrt{2}$不符合题意,舍去,
∴m=5-$\sqrt{2}$;
②点P在线段AB上,点Q在线段CB上(4<x<6),
设经过n秒,依题意有
$\frac{1}{2}$(6-n)(2n-8)=1,
m2-10n+25=0,
解得n1=n2=5,
经检验,n=5符合题意.
③点P在射线AB上,点Q在射线CB上(x>6),
设经过k秒,依题意有
$\frac{1}{2}$(k-6)(2k-8)=1,
k2-10k+23=0,
解得k1=5+$\sqrt{2}$,k2=5-$\sqrt{2}$,
经检验,k1=5-$\sqrt{2}$不符合题意,舍去,
∴k=5+$\sqrt{2}$;
综上所述,经过(5-$\sqrt{2}$)秒,5秒,(5+$\sqrt{2}$)秒后,△PBQ的面积为1.
点评 考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.注意分类思想的运用.

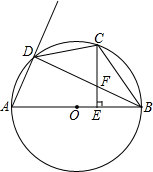 如图,AB是⊙O的直径,C是弧BD的中点,CE⊥AB,垂足为E,BD交CE于点F.
如图,AB是⊙O的直径,C是弧BD的中点,CE⊥AB,垂足为E,BD交CE于点F.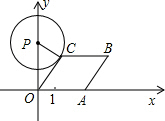 如图所示,已知A点从(1,0)点出发,以每秒1个单位长的速度沿着x轴的正方向运动,以O、A为顶点作菱形OABC,使B、C点都在第一象限内,且∠AOC=60°.设经过t秒后,以P(0,3)为圆心,PC为半径的圆恰好与菱形OABC的边所在的直线相切,则t=$\frac{3\sqrt{3}}{2}$-1或$3\sqrt{3}-1$.
如图所示,已知A点从(1,0)点出发,以每秒1个单位长的速度沿着x轴的正方向运动,以O、A为顶点作菱形OABC,使B、C点都在第一象限内,且∠AOC=60°.设经过t秒后,以P(0,3)为圆心,PC为半径的圆恰好与菱形OABC的边所在的直线相切,则t=$\frac{3\sqrt{3}}{2}$-1或$3\sqrt{3}-1$.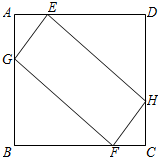 如图,边长为4的正方形ABCD中,AE=CF=1,点G、H分别是边AB、CD上的动点,且AG=CH.
如图,边长为4的正方形ABCD中,AE=CF=1,点G、H分别是边AB、CD上的动点,且AG=CH.