题目内容
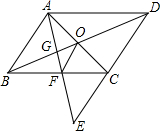 如图,E为?ABCD中DC边的延长线上一点,CE=CD,AE交BC于F,AC交BD于O,连接OF.
如图,E为?ABCD中DC边的延长线上一点,CE=CD,AE交BC于F,AC交BD于O,连接OF.(1)求证:△ABF≌△ECF;
(2)探究OF与DE的数量关系.
考点:平行四边形的性质,全等三角形的判定与性质
专题:
分析:(1)由AB∥CD可以得到∠BAF=∠E,∠ABF=∠ECF,再利用DC=CE即可证明△ABF≌△ECF;
(2)根据(1)的结论知道BF=CF,AB=CE,而AO=CO,由此利用中位线定理即可证明题目结论.
(2)根据(1)的结论知道BF=CF,AB=CE,而AO=CO,由此利用中位线定理即可证明题目结论.
解答:证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
又∵DC=CE,
∴AB=CE.
∵AB∥CD,
∴∠BAF=∠E,∠ABF=∠ECF.
∴△ABF≌△ECF;
(2)∵△ABF≌△ECF,
∴BF=CF,AB=CE,
又∵四边形ABCD是平行四边形,
∴AO=CO,AB=CE,
∴OF是△ABC的中位线,
∴CE=2OF,
∵DE=AB+CE=2CE,
∴DE=4OF.
∴AB∥CD,AB=CD.
又∵DC=CE,
∴AB=CE.
∵AB∥CD,
∴∠BAF=∠E,∠ABF=∠ECF.
∴△ABF≌△ECF;
(2)∵△ABF≌△ECF,
∴BF=CF,AB=CE,
又∵四边形ABCD是平行四边形,
∴AO=CO,AB=CE,
∴OF是△ABC的中位线,
∴CE=2OF,
∵DE=AB+CE=2CE,
∴DE=4OF.
点评:本题考查的是平行四边形的性质及三角形的中位线定理,利用平行四边形的性质,获得全等的条件是解题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
若方程x2-3x-1=0的两根为x1、x2,则
的值为( )
| x1+x2 |
| x1x2 |
| A、3 | ||
| B、-3 | ||
C、
| ||
D、-
|
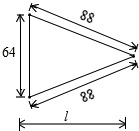 已知一个工件尺寸如图(单位:mm),计算l的长(精确到1mm).
已知一个工件尺寸如图(单位:mm),计算l的长(精确到1mm). 如图,某装置有一枚指针,原来指向南偏西50°,把这枚指针按顺时针方向旋转90°.
如图,某装置有一枚指针,原来指向南偏西50°,把这枚指针按顺时针方向旋转90°.