题目内容
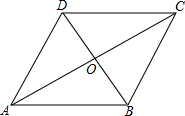
如图所示，四边形ABCD中，给出下列三个判断：①AD∥BC，②BD2=AD•BC，③∠ABD+∠ADC=180°，请你从其中选取两个条件，另一个做结论构成一个真命题且加以证明．考点：命题与定理,相似三角形的判定与性质
专题：
分析：利用平行线的性质结合相似三角形的判定与性质得出△ABD∽△DCB，进而得出答案．
解答：解：当已知：①AD∥BC，③∠ABD+∠ADC=180°，结论：②BD2=AD•BC，
理由：∵AD∥BC，
∴∠ADB=∠DBC，∠ADC+∠C=180°，
∵∠ABD+∠ADC=180°，
∴∠C=∠ABD，
∴△ABD∽△DCB，
∴
=
，
∴BD2=AD•BC．
理由：∵AD∥BC，
∴∠ADB=∠DBC，∠ADC+∠C=180°，
∵∠ABD+∠ADC=180°，
∴∠C=∠ABD，
∴△ABD∽△DCB，
∴
| BD |
| BC |
| AD |
| BD |
∴BD2=AD•BC．
点评：此题主要考查了相似三角形的判定与性质，根据题意得出△ABD∽△DCB是解题关键．
练习册系列答案
相关题目
如图，OC平分∠AOB，CD⊥OB于D，点P是射线OA上的一个动点，若CD=8，OD=6，则PC的最小值为（ ）| A、6 | B、7 | C、8 | D、10 |
若方程x2-3x-1=0的两根为x1、x2，则
的值为（ ）
| x1+x2 |
| x1x2 |
| A、3 | ||
| B、-3 | ||
C、
| ||
D、-
|
如图所示，四边形ABCD的两条对角线AC、BD相交于点O，AB=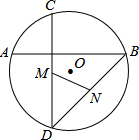
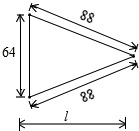已知一个工件尺寸如图（单位：mm），计算l的长（精确到1mm）．