题目内容
2.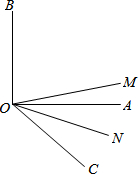 已知:如图,ON平分∠AOC,OM平分∠BOC,∠AOB=90°;
已知:如图,ON平分∠AOC,OM平分∠BOC,∠AOB=90°;(1)∠AOC=40°,求∠MON的大小;
(2)当锐角∠AOC的度数发生改变时,∠MON的大小是否发生改变,并说明理由.
分析 (1)求得∠BOC=130°,然后求得∠NOC=$\frac{1}{2}$∠AOC=20°,∠MOC=$\frac{1}{2}$∠BOC=65°,根据∠MON=∠MOC-∠NOC即可求出∠MON的度数.
(2)结合图形,根据角的和差,以及角平分线的定义,找到∠MON与∠AOB的关系,即可求出∠MON的度数.
解答 解:(1)∵∠AOB=90°,∠AOC=40°,
∴∠BOC=130°,
∵ON平分∠AOC,OM平分∠BOC,
∴∠NOC=$\frac{1}{2}$∠AOC=20°,∠MOC=$\frac{1}{2}$∠BOC=65°,
∴∠MON=∠MOC-∠NOC=65°-20°=45°,
即∠MON=45°;
(2)不发生改变,
理由:∵OM平分∠BOC,ON平分∠AOC,
∴∠MOC=$\frac{1}{2}$∠BOC,∠NOC=$\frac{1}{2}$∠AOC,
∴∠MON=∠MOC-∠NOC=$\frac{1}{2}$(∠BOC-∠AOC)
=$\frac{1}{2}$(∠AOB+∠AOC-∠AOC)
=$\frac{1}{2}$∠AOB
=45°.
所以不发生改变.
点评 本题考查了角的计算,属于基础题,此类问题,注意结合图形,运用角的和差和角平分线的定义求解.

练习册系列答案
相关题目
11.七(1)班第3组有10名同学,其身高如下表:
请用简便方法求这组同学的总身高.
| 学号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 身高/cm | 152 | 163 | 169 | 153 | 154 | 167 | 155 | 164 | 157 | 161 |
11.从分别写有数字-4,-3,-2,-1,3,4的六张卡片中,任意抽取一张,则所抽卡片上数字的绝对值小于2的概率是( )
| A. | $\frac{1}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
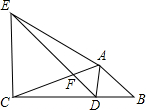 如图,在△ABC中,将△ABC绕点A顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上,且DE∥AB交AC于F时.
如图,在△ABC中,将△ABC绕点A顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上,且DE∥AB交AC于F时.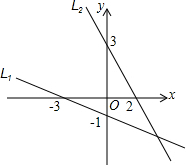 如图,L1,L2的交点坐标可以看成方程组:$\left\{\begin{array}{l}{y=-\frac{1}{3}x-1}\\{y=-\frac{3}{2}x+3}\end{array}\right.$的解.
如图,L1,L2的交点坐标可以看成方程组:$\left\{\begin{array}{l}{y=-\frac{1}{3}x-1}\\{y=-\frac{3}{2}x+3}\end{array}\right.$的解. 在平面直角坐标系xOy中,直线y=-2x+1与y轴交于点C,直线y=x+k(k≠0)与y轴交于点A,与直线y=-2x+1交于点B,设点B的横坐标为x0.
在平面直角坐标系xOy中,直线y=-2x+1与y轴交于点C,直线y=x+k(k≠0)与y轴交于点A,与直线y=-2x+1交于点B,设点B的横坐标为x0.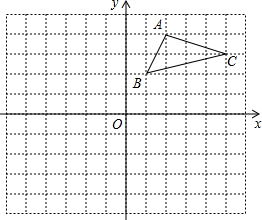 如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题: