题目内容
17.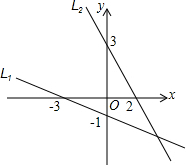 如图,L1,L2的交点坐标可以看成方程组:$\left\{\begin{array}{l}{y=-\frac{1}{3}x-1}\\{y=-\frac{3}{2}x+3}\end{array}\right.$的解.
如图,L1,L2的交点坐标可以看成方程组:$\left\{\begin{array}{l}{y=-\frac{1}{3}x-1}\\{y=-\frac{3}{2}x+3}\end{array}\right.$的解.
分析 运用待定系数法分别求出两条直线的解析式,根据一次函数与二元一次方程组的关系解答即可.
解答 解:∵L1经过点(-3,0),(0,-1),
设L1的解析式为y=kx+b,
则$\left\{\begin{array}{l}{-3k+b=0}\\{b=-1}\end{array}\right.$,
解得k=-$\frac{1}{3}$,b=-1,
∴设L1的解析式为y=-$\frac{1}{3}$x-1;
设L2的解析式为y=ax+c,
则$\left\{\begin{array}{l}{2a+c=0}\\{c=3}\end{array}\right.$,
解得,a=-$\frac{3}{2}$,c=3,
∴L1的解析式为y=-$\frac{3}{2}$x+3,
∴L1,L2的交点坐标可以看成方程组$\left\{\begin{array}{l}{y=-\frac{1}{3}x-1}\\{y=-\frac{3}{2}x+3}\end{array}\right.$的解,
故答案为:$\left\{\begin{array}{l}{y=-\frac{1}{3}x-1}\\{y=-\frac{3}{2}x+3}\end{array}\right.$.
点评 本题考查的是一次函数与二元一次方程组的关系以及待定系数法求函数解析式,理解两直线的交点是二元一次方程组的解是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.三角形的重心是( )
| A. | 三角形三边垂直平分线的交点 | B. | 三角形三边上高所在直线的交点 | ||
| C. | 三角形三边上中线的交点 | D. | 三角形三个内角平分线的交点 |
6.计算$\frac{1}{2}$×(-2)÷(-$\frac{1}{2}$)×(-2)的结果为( )
| A. | -4 | B. | -2 | C. | -3 | D. | -1 |
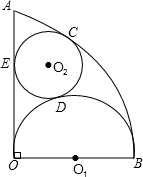 如图,扇形AOB的半径为4,∠AOB=90°,O1是以OB为直径的半圆的圆心,⊙O2与$\widehat{AB}$、半圆O1、OA分别相切于点C、D、E,求⊙O2的半径.
如图,扇形AOB的半径为4,∠AOB=90°,O1是以OB为直径的半圆的圆心,⊙O2与$\widehat{AB}$、半圆O1、OA分别相切于点C、D、E,求⊙O2的半径.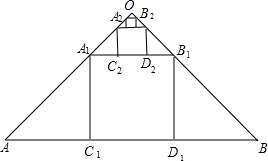 如图,在斜边长为1的等腰直角三角形OAB中,作内接正方形A1B1C1D1;在等腰直角三角形OA1B1中,作内接正方形A2B2C2D2;在等腰直角三角形OA2B2中,作内接正方形A3B3C3D3…;依次作下去,则第2015个正方形A2015B2015C2015D2015的边长是$(\frac{1}{3})^{2015}$.
如图,在斜边长为1的等腰直角三角形OAB中,作内接正方形A1B1C1D1;在等腰直角三角形OA1B1中,作内接正方形A2B2C2D2;在等腰直角三角形OA2B2中,作内接正方形A3B3C3D3…;依次作下去,则第2015个正方形A2015B2015C2015D2015的边长是$(\frac{1}{3})^{2015}$.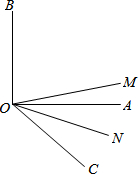 已知:如图,ON平分∠AOC,OM平分∠BOC,∠AOB=90°;
已知:如图,ON平分∠AOC,OM平分∠BOC,∠AOB=90°;