题目内容
14.已知关于x的方程x2-mx-m2=0(m为实数).(1)试说明方程一定有两个实数根;
(2)若方程的两实数根中,绝对值较大的根为1,求m.
分析 (1)先计算判别式的值得到△=5m2,利用非负数的性质得△≥0,则根据判别式的意义可判断方程有两个两个实数根;
(2)利用公式法解方程得到x=$\frac{1±\sqrt{5}}{2}$m,利用绝对值较大的根为1得到$\frac{1+\sqrt{5}}{2}$m=1,然后解方程求出m即可.
解答 解:(1)△=(-m)2-4(-m2)
=5m2,
∵5m2≥0,即△≥0,
∴方程有两个两个实数根;
(2)x=$\frac{m±\sqrt{5}m}{2}$=$\frac{1±\sqrt{5}}{2}$m,
∵绝对值较大的根为1,
∴$\frac{1+\sqrt{5}}{2}$m=1,
∴m=$\frac{-1+\sqrt{5}}{2}$.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.也考查了解一元二次方程-公式法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.三角形的重心是( )
| A. | 三角形三边垂直平分线的交点 | B. | 三角形三边上高所在直线的交点 | ||
| C. | 三角形三边上中线的交点 | D. | 三角形三个内角平分线的交点 |
6.计算$\frac{1}{2}$×(-2)÷(-$\frac{1}{2}$)×(-2)的结果为( )
| A. | -4 | B. | -2 | C. | -3 | D. | -1 |
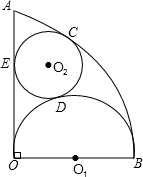 如图,扇形AOB的半径为4,∠AOB=90°,O1是以OB为直径的半圆的圆心,⊙O2与$\widehat{AB}$、半圆O1、OA分别相切于点C、D、E,求⊙O2的半径.
如图,扇形AOB的半径为4,∠AOB=90°,O1是以OB为直径的半圆的圆心,⊙O2与$\widehat{AB}$、半圆O1、OA分别相切于点C、D、E,求⊙O2的半径.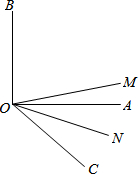 已知:如图,ON平分∠AOC,OM平分∠BOC,∠AOB=90°;
已知:如图,ON平分∠AOC,OM平分∠BOC,∠AOB=90°;