题目内容
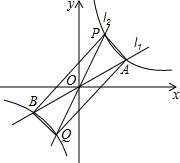 如图,经过原点的两条直线l1、l2分别与双曲线y=
如图,经过原点的两条直线l1、l2分别与双曲线y=| k |
| x |
(1)求k值及B点坐标;
(2)若P点坐标为(a,3),求a值及四边形APBQ的面积;
(3)若P点坐标为(m,n),且∠APB=90°,求P点坐标.
考点:反比例函数综合题
专题:综合题
分析:(1)根据分别莲花山图象上点的坐标特征得到k=3×1=3,再根据正比例函数图象和反比例函数图象的性质得到点A与点B关于原点对称,则B点坐标为(-3,-1);
(2)先根据反比例函数图象上点的坐标特征得到a=1,即P点坐标为(1,3),再根据正比例函数图象和反比例函数图象的性质得到点P与点Q关于原点对称,所以点Q的坐标为(-1,-3),由于OA=OB,OP=OQ,则根据平行四边形的判定得到四边形APBQ为平行四边形,然后根据两点间的距离公式计算出AB,PQ,可得到即AB=PQ,于是可判断四边形APBQ为矩形,再计算出PA和PB,然后计算矩形APBQ的面积;
(3)前面已经证明四边形APBQ为平行四边形,加上∠APB=90°,则可判断四边形APBQ为矩形,则OP=OA,根据两点间的距离公式得到m2+n2=10,且mn=3,则利用完全平方公式得到(m+n)2-2mn=10,可得到m+n=4,根据根与系数的关系可把m、n看作方程x2-4x+3=0的两根,然后解方程可得到满足条件的P点坐标.
(2)先根据反比例函数图象上点的坐标特征得到a=1,即P点坐标为(1,3),再根据正比例函数图象和反比例函数图象的性质得到点P与点Q关于原点对称,所以点Q的坐标为(-1,-3),由于OA=OB,OP=OQ,则根据平行四边形的判定得到四边形APBQ为平行四边形,然后根据两点间的距离公式计算出AB,PQ,可得到即AB=PQ,于是可判断四边形APBQ为矩形,再计算出PA和PB,然后计算矩形APBQ的面积;
(3)前面已经证明四边形APBQ为平行四边形,加上∠APB=90°,则可判断四边形APBQ为矩形,则OP=OA,根据两点间的距离公式得到m2+n2=10,且mn=3,则利用完全平方公式得到(m+n)2-2mn=10,可得到m+n=4,根据根与系数的关系可把m、n看作方程x2-4x+3=0的两根,然后解方程可得到满足条件的P点坐标.
解答:解:(1)把A(3,1)代入y=
得k=3×1=3,
∵经过原点的直线l1与双曲线y=
(k≠0)相交于A、B、
∴点A与点B关于原点对称,
∴B点坐标为(-3,-1);
(2)把P(a,3)代入y=
得3a=3,解得a=1,
∵P点坐标为(1,3),
∵经过原点的直线l2与双曲线y=
(k≠0)相交于P、Q点,
∴点P与点Q关于原点对称,
∴点Q的坐标为(-1,-3),
∵OA=OB,OP=OQ,
∴四边形APBQ为平行四边形,
∵AB2=(3+3)2+(1+1)2=40,PA2=(1+1)2+(3+3)2=40,
∴AB=PQ,
∴四边形APBQ为矩形,
∵PB2=(1+3)2+(3+1)2=32,PQ2=(3-1)2+(1-3)2=8,
∴PB=4
,PQ=2
,
∴四边形APBQ的面积=PA•PB=2
•4
=16;
(3)∵四边形APBQ为平行四边形,
而∠APB=90°,
∴四边形APBQ为矩形,
∴OP=OA,
∴m2+n2=32+12=10,
而mn=3,
∵(m+n)2-2mn=10,
∴(m+n)2=16,解得m+n=4或m+n=-4(舍去),
把m、n看作方程x2-4x+3=0的两根,解得m=1,n=3或m=3,n=1(舍去),
∴P点坐标为(1,3).
| k |
| x |
∵经过原点的直线l1与双曲线y=
| k |
| x |
∴点A与点B关于原点对称,
∴B点坐标为(-3,-1);
(2)把P(a,3)代入y=
| 3 |
| x |
∵P点坐标为(1,3),
∵经过原点的直线l2与双曲线y=
| k |
| x |
∴点P与点Q关于原点对称,
∴点Q的坐标为(-1,-3),
∵OA=OB,OP=OQ,
∴四边形APBQ为平行四边形,
∵AB2=(3+3)2+(1+1)2=40,PA2=(1+1)2+(3+3)2=40,
∴AB=PQ,
∴四边形APBQ为矩形,
∵PB2=(1+3)2+(3+1)2=32,PQ2=(3-1)2+(1-3)2=8,
∴PB=4
| 2 |
| 2 |
∴四边形APBQ的面积=PA•PB=2
| 2 |
| 2 |
(3)∵四边形APBQ为平行四边形,
而∠APB=90°,
∴四边形APBQ为矩形,
∴OP=OA,
∴m2+n2=32+12=10,
而mn=3,
∵(m+n)2-2mn=10,
∴(m+n)2=16,解得m+n=4或m+n=-4(舍去),
把m、n看作方程x2-4x+3=0的两根,解得m=1,n=3或m=3,n=1(舍去),
∴P点坐标为(1,3).
点评:本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征、正比例函数图象与反比例函数图象的性质、等腰三角形的性质、矩形的判定与性质;会利用两点间的距离公式计算线段的长;理解坐标与图形的性质.

练习册系列答案
相关题目
 请填空完成下面的证明:
请填空完成下面的证明: 如图,BD是平行四边形?ABCD的对角线,E、F在BD上.
如图,BD是平行四边形?ABCD的对角线,E、F在BD上. 如图,在矩形ABCD中,AB=3,BC=4,BE⊥AC,垂足为点E,试求BE的长.
如图,在矩形ABCD中,AB=3,BC=4,BE⊥AC,垂足为点E,试求BE的长. 如图,在△ABC中,∠B和∠C的平分线相交于点P,∠A=64°,则∠P=
如图,在△ABC中,∠B和∠C的平分线相交于点P,∠A=64°,则∠P=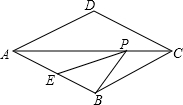 如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,当P移动到AC的中点时,则PE+PB的值是
如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,当P移动到AC的中点时,则PE+PB的值是