题目内容
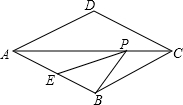 如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,当P移动到AC的中点时,则PE+PB的值是
如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,当P移动到AC的中点时,则PE+PB的值是考点:菱形的性质
专题:
分析:找出B点关于AC的对称点D,连接PE,进而判断△PEB是等边三角形,求出PE+PB的值即可.
解答: 解:连接BD交AC于P,连接PE,
解:连接BD交AC于P,连接PE,
由菱形的对角线互相垂直平分,可得B、D关于AC对称,则PD=PB,∠APB=90°,
∴PE=
AB=1,
∵∠BAD=60°,AD=AB,
∴△ABD是等边三角形,
∴∠ABD=60°,
∵AE=BE,
∴PE=BE,
∴△BEP是等边三角形,
∴PE=PB=1,
∴PE+PB的值是2.
故答案为:2.
 解:连接BD交AC于P,连接PE,
解:连接BD交AC于P,连接PE,由菱形的对角线互相垂直平分,可得B、D关于AC对称,则PD=PB,∠APB=90°,
∴PE=
| 1 |
| 2 |
∵∠BAD=60°,AD=AB,
∴△ABD是等边三角形,
∴∠ABD=60°,
∵AE=BE,
∴PE=BE,
∴△BEP是等边三角形,
∴PE=PB=1,
∴PE+PB的值是2.
故答案为:2.
点评:本题主要考查了菱形的性质,解答本题的关键是得出△BEP是等边三角形.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
若P=(x-2)(x-4),Q=(x-3)2,则P与Q的关系为( )
| A、P=Q | B、P>Q |
| C、P<Q | D、P与Q的大小无法确定 |
 如图,点P是函数y=
如图,点P是函数y= 如图,经过原点的两条直线l1、l2分别与双曲线y=
如图,经过原点的两条直线l1、l2分别与双曲线y= 如图,平行四边形ABCD的周长为40,△BOC的周长比△AOB的周长多10,则AB为
如图,平行四边形ABCD的周长为40,△BOC的周长比△AOB的周长多10,则AB为