题目内容
 如图,在矩形ABCD中,AB=3,BC=4,BE⊥AC,垂足为点E,试求BE的长.
如图,在矩形ABCD中,AB=3,BC=4,BE⊥AC,垂足为点E,试求BE的长.考点:矩形的性质,勾股定理
专题:
分析:利用勾股定理求得AC的长度,然后利用面积法来求BE的长度.
解答: 解:如图,在矩形ABCD中,∠ABC=90°,AC=
解:如图,在矩形ABCD中,∠ABC=90°,AC=
=
=5.
又∵△ABC的面积为:
AB•BC=
AC•BE,
∴BE=
=
=2.4.
 解:如图,在矩形ABCD中,∠ABC=90°,AC=
解:如图,在矩形ABCD中,∠ABC=90°,AC=| AB2+BC2 |
| 32+42 |
又∵△ABC的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
∴BE=
| AB•BC |
| AC |
| 3×4 |
| 5 |
点评:本题考查了矩形的性质和勾股定理.此题利用△ABC的面积是定值列出等式
AB•BC=
AC•BE,从而求得BE的长度.
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目

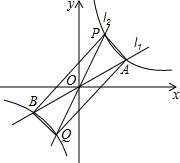 如图,经过原点的两条直线l1、l2分别与双曲线y=
如图,经过原点的两条直线l1、l2分别与双曲线y= 如图,平行四边形ABCD的周长为40,△BOC的周长比△AOB的周长多10,则AB为
如图,平行四边形ABCD的周长为40,△BOC的周长比△AOB的周长多10,则AB为