题目内容
已知不等式组
的解集中任意x的值都不在1<x≤4的范围内,则m的取值范围是 .
|
考点:解一元一次不等式组
专题:
分析:首先解不等式得到不等式组的解集,然后根据任意x的值都不在1<x≤4的范围内,即可得到关于m的不等式,从而求得m的范围.
解答:解:
,
解①得:x>m-1,
解②得:x≤m,
则m-1<x≤m,
∵不等式的解都不在1<x≤4内,
∴m≤1或m-1≥4,
即m≤1或m≥5.
答案是:m≤1或m≥5.
|
解①得:x>m-1,
解②得:x≤m,
则m-1<x≤m,
∵不等式的解都不在1<x≤4内,
∴m≤1或m-1≥4,
即m≤1或m≥5.
答案是:m≤1或m≥5.
点评:本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.还可以观察不等式的解,若x>较小的数、<较大的数,那么解集为x介于两数之间.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
若P=(x-2)(x-4),Q=(x-3)2,则P与Q的关系为( )
| A、P=Q | B、P>Q |
| C、P<Q | D、P与Q的大小无法确定 |
下列各式一定成立的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
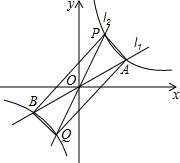 如图,经过原点的两条直线l1、l2分别与双曲线y=
如图,经过原点的两条直线l1、l2分别与双曲线y=