题目内容
 如图,在△ABC中,∠B和∠C的平分线相交于点P,∠A=64°,则∠P=
如图,在△ABC中,∠B和∠C的平分线相交于点P,∠A=64°,则∠P=考点:三角形内角和定理,角平分线的定义
专题:
分析:先根据三角形内角和定理求出∠ABC+∠ACB的度数,再由角平分线的定义得出∠PBC+∠PCB的度数,根据三角形内角和定理即可得出结论.
解答:解:∵△ABC中,∠A=64°,
∴∠ABC+∠ACB=180°-∠A=180°-64°=116°,
∵△ABC的两内角平分线相交于点P,
∴∠PBC+∠PCB=
(∠ABC+∠ACB)=
×116°=58°,
∴∠P=180°-(∠PBC+∠PCB)=180°-58°=122°.
故答案为:122°.
∴∠ABC+∠ACB=180°-∠A=180°-64°=116°,
∵△ABC的两内角平分线相交于点P,
∴∠PBC+∠PCB=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠P=180°-(∠PBC+∠PCB)=180°-58°=122°.
故答案为:122°.
点评:本题考查的是三角形内角和定理及角平分线的定义,熟知三角形的内角和是180°是解答此题的关键.

练习册系列答案
相关题目
 如图,直线AB、CD相交于点O,EO⊥AB,垂足为O,∠EOC=35°,求∠AOD的度数.
如图,直线AB、CD相交于点O,EO⊥AB,垂足为O,∠EOC=35°,求∠AOD的度数.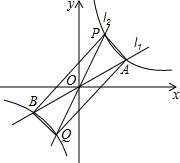 如图,经过原点的两条直线l1、l2分别与双曲线y=
如图,经过原点的两条直线l1、l2分别与双曲线y= 如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东85°方向,则∠ACB的度数为
如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东85°方向,则∠ACB的度数为 如图,平行四边形ABCD的周长为40,△BOC的周长比△AOB的周长多10,则AB为
如图,平行四边形ABCD的周长为40,△BOC的周长比△AOB的周长多10,则AB为