题目内容
 请填空完成下面的证明:
请填空完成下面的证明:如图,点D、E、F分别是三角形ABC的边BC、CA、AB上的点,DE∥BA,∠A=∠FDE.
求证:DF∥AC.
证明:∵DE∥BA
∴∠A=
∵∠A=∠FDE
∴∠FDE=
∴DF∥AC(
考点:平行线的判定与性质
专题:推理填空题
分析:根据平行线的性质得出∠A=∠DEC,求出∠FDE=∠DEC,根据平行线的判定推出即可.
解答:证明:∵DE∥BA,
∴∠A=∠DEC(两直线平行,同位角相等),
∵∠A=∠FDE(已知),
∴∠FDE=∠DEC(等量代换),
∴DF∥AC(内错角相等,两直线平行),
故答案为:∠DEC,两直线平行,同位角相等;∠DEC,内错角相等,两直线平行.
∴∠A=∠DEC(两直线平行,同位角相等),
∵∠A=∠FDE(已知),
∴∠FDE=∠DEC(等量代换),
∴DF∥AC(内错角相等,两直线平行),
故答案为:∠DEC,两直线平行,同位角相等;∠DEC,内错角相等,两直线平行.
点评:本题考查了平行线的性质和判定的应用,注意:①两直线平行,同位角相等,②内错角相等,两直线平行.

练习册系列答案
相关题目
 如图,点P是函数y=
如图,点P是函数y= 如图,直线AB、CD相交于点O,EO⊥AB,垂足为O,∠EOC=35°,求∠AOD的度数.
如图,直线AB、CD相交于点O,EO⊥AB,垂足为O,∠EOC=35°,求∠AOD的度数.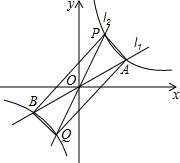 如图,经过原点的两条直线l1、l2分别与双曲线y=
如图,经过原点的两条直线l1、l2分别与双曲线y=