题目内容
 如图,已知PA是⊙O的切线,P为切点,PA=5
如图,已知PA是⊙O的切线,P为切点,PA=5| 3 |
考点:切线的性质
专题:
分析:根据切线的性质判定△APO是直角三角形,则利用勾股定理来求该圆的半径即可.
解答:解:如图,∵PA是⊙O的切线,P为切点,
∴AP⊥OP,
∴∠APO=90°.
又∵PA=5
,AB=5,OP=OB,
则AP2+OP2=(AB+OP)2,即75+OP2=(5+OP)2,
解得 OP=5.
故答案是:5.
∴AP⊥OP,

∴∠APO=90°.
又∵PA=5
| 3 |
则AP2+OP2=(AB+OP)2,即75+OP2=(5+OP)2,
解得 OP=5.
故答案是:5.
点评:本题考查了切线的性质.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
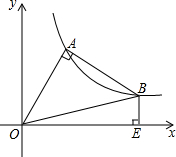 △OAB在第一象限中,OA=AB,OA⊥AB,O是坐标原点,且函数y=
△OAB在第一象限中,OA=AB,OA⊥AB,O是坐标原点,且函数y= 表示a、b、c三个数的点在数轴上如图所示,化简:|a-b|+|b-c|-|c-a|+|b+c|.
表示a、b、c三个数的点在数轴上如图所示,化简:|a-b|+|b-c|-|c-a|+|b+c|. 如图,在△ABC中,AD是边BC上的高,AC=BD,已知sinC=
如图,在△ABC中,AD是边BC上的高,AC=BD,已知sinC= 如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,DE=2
如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,DE=2
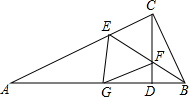 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,BE平分∠ABC交AC于E,交CD于F,FG∥CA于G,求证:四边形CEGF是菱形.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,BE平分∠ABC交AC于E,交CD于F,FG∥CA于G,求证:四边形CEGF是菱形.