题目内容
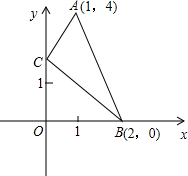 在平面直角坐标系中,已知两点A(1,4)B(2,0),点C是y轴上的一个动点,且A、B、C三点不共线,求△ABC周长的最小值及相应点C的坐标.
在平面直角坐标系中,已知两点A(1,4)B(2,0),点C是y轴上的一个动点,且A、B、C三点不共线,求△ABC周长的最小值及相应点C的坐标.考点:轴对称-最短路线问题,坐标与图形性质
专题:
分析:作B点关于y轴对称点B′点,连接AB′,交y轴于点C′,此时△ABC的周长最小,根据平行线分线段成比例定理就可求得OC′即可得出△ABC的周长最小时C点坐标,进而根据勾股定理就可求出△ABC的周长.
解答: 解:作B点关于y轴对称点B′点,连接AB′,交y轴于点C′,
解:作B点关于y轴对称点B′点,连接AB′,交y轴于点C′,
此时△ABC的周长最小,
∵点A、B的坐标分别为(1,4)和(2,0),
∴B′点坐标为:(-2,0),AE=4,
则B′E=3,
∵C′O∥AE,
∴
=
,
即
=
,
∴C′O=
,
∴点C′的坐标是(0,
),此时△ABC的周长最小值=AB′+AB=
+
=5+
.
 解:作B点关于y轴对称点B′点,连接AB′,交y轴于点C′,
解:作B点关于y轴对称点B′点,连接AB′,交y轴于点C′,此时△ABC的周长最小,
∵点A、B的坐标分别为(1,4)和(2,0),
∴B′点坐标为:(-2,0),AE=4,
则B′E=3,
∵C′O∥AE,
∴
| B′O |
| B′E |
| OC′ |
| AE |
即
| 2 |
| 3 |
| OC′ |
| 4 |
∴C′O=
| 8 |
| 3 |
∴点C′的坐标是(0,
| 8 |
| 3 |
| 32+42 |
| (2-1)2+(4-0)2 |
| 17 |
点评:此题主要考查了利用轴对称求最短路线以及平行线的性质和勾股定理的运用,根据已知得出C点位置是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,Rt△ABC中,∠C=90°,AC=2,BC=5.分别以AB、AC、BC为边在AB的同侧作正方形ABEF,ACPQ,BDMC,四块阴影部分的面积分别为S1,S2,S3,S4.则S1+S2+S3+S4等于( )
如图,Rt△ABC中,∠C=90°,AC=2,BC=5.分别以AB、AC、BC为边在AB的同侧作正方形ABEF,ACPQ,BDMC,四块阴影部分的面积分别为S1,S2,S3,S4.则S1+S2+S3+S4等于( )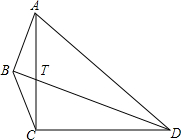 在四边形ABCD中,AC⊥CD,AC=CD,∠ABD=90°,BD平分∠APC,交AC于点T.求证:DT=2AB.
在四边形ABCD中,AC⊥CD,AC=CD,∠ABD=90°,BD平分∠APC,交AC于点T.求证:DT=2AB.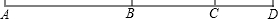 已知:B是线段上AC上一点,且AB:BC=10:7,D是线段AC延长线上一点,且BD:AC=11:17,若CD=16,求BC的长.
已知:B是线段上AC上一点,且AB:BC=10:7,D是线段AC延长线上一点,且BD:AC=11:17,若CD=16,求BC的长.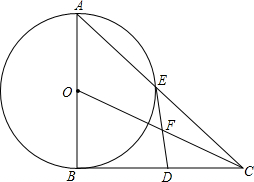 如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点E,点D是BC边上的中点,连接DE.
如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点E,点D是BC边上的中点,连接DE. 如图,AB为⊙O的直径,点C为⊙O上一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.
如图,AB为⊙O的直径,点C为⊙O上一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.