题目内容
 在Rt△ABC中,∠C=90°,cosB=
在Rt△ABC中,∠C=90°,cosB=| 3 |
| 5 |
考点:互余两角三角函数的关系
专题:
分析:根据互为余角的三角函数关系,可得sinA,根据正弦等于对边比斜边,可得BC与AB的关系,根据勾股定理,可得AC的长 再根据正切等于对边比邻边,可得答案.
解答:解:由在Rt△ABC中,∠C=90°,cosB=
,得
sinA=cosB=
=
,
设BC=3x,AB=4x,勾股定理得
AC=
=4x,
由正切等于对边比邻边,得
tanA=
=
=
.
| 3 |
| 5 |
sinA=cosB=
| BC |
| AB |
| 3 |
| 5 |
设BC=3x,AB=4x,勾股定理得
AC=
| AB2-BC2 |
由正切等于对边比邻边,得
tanA=
| BC |
| AC |
| 3x |
| 4x |
| 3 |
| 4 |
点评:本题考查了互为余角三角函数的关系,利用了互余两角三角函数的关系,勾股定理,正切函数的定义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
二次函数y=-3(x-2)2+4的最大值是( )
| A、2 | B、-2 | C、-3 | D、4 |
若二次函数y=(a+1)x2+3x+a2-1的图象经过原点,则a的值必为( )
| A、1或-1 | B、1 | C、-1 | D、0 |
图象与二次函数y=x2-2x+3的图象关于x=-1直线对称的二次函数是( )
| A、y=x2-2x+3 |
| B、y=x2+6x+11 |
| C、y=x2_2x+11 |
| D、y=x2+6x-3 |
已知圆锥的底面半径为6,母线长为8,圆锥的侧面积为( )
| A、60 | B、48 |
| C、60π | D、48π |
 如图,AB为⊙O的直径,点C为⊙O上一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.
如图,AB为⊙O的直径,点C为⊙O上一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.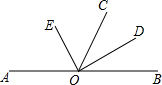 已知:A、O、B三点在同一直线上,OE、OD分别平分∠AOC、∠BOC.
已知:A、O、B三点在同一直线上,OE、OD分别平分∠AOC、∠BOC. 在正方形ABCD中,E是AD中点,F是CD上点,且CF=3DF,连接EF,EB,求证:△ABE∽△DEF.
在正方形ABCD中,E是AD中点,F是CD上点,且CF=3DF,连接EF,EB,求证:△ABE∽△DEF. 如图,人们明明知道就践踏草坪是不文明的行为,但在生活中还是常常出现这种现象,我们可以用
如图,人们明明知道就践踏草坪是不文明的行为,但在生活中还是常常出现这种现象,我们可以用