题目内容
3.某商场将进价为30元的台灯按40元出售,平均每月能售出600盏.调查表明,这种台灯的售价每上涨1元,其销售量减少10盏.为了实现平均每月10000元的销售利润,这种台灯的售价应定为多少元?这时应进台灯多少盏?分析 设这种台灯的售价定为x元,那么就少卖出10(x-40)个,根据利润=售价-进价,可列方程求解.
解答 解:设这种台灯的售价定为x元,由题意得
[600-10(x-40)](x-30)=10000,
整理,得x2-130x+4000=0,
解得:x1=50,x2=80.
当x=50时,600-10(x-40)=600-10×(50-40)=500(个);
当x=80时,600-10(x-40)=600-10×(80-40)=200(个).
答:台灯的定价定为50元,这时应进台灯500个;台灯的定价定为80元,这时应进台灯200个.
点评 本题考查一元二次方程的应用,关键是看到定价和销售量的关系,根据利润列方程求解.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
11.下列说法正确的是( )
| A. | “明天降雨的概率是80%”表示明天有80%的时间降雨 | |
| B. | “抛一枚硬币正面朝上的概率是0.5”表示每抛硬币2次就有1次出现正面朝上 | |
| C. | 在一个装着白球和黑球的袋中摸球,摸出红球是随机事件 | |
| D. | 掷一枚质地均匀的骰子,朝上一面的点数是7是确定事件 |
18.下列命题是真命题的是( )
| A. | 四条边都相等的四边形是矩形 | |
| B. | 菱形的对角线相等 | |
| C. | 对角线互相垂直的平行四边形是正方形 | |
| D. | 对角线相等且互相平分的四边形是矩形 |
15.如果2是一元二次方程x2=x+c的一个根,那么常数c是( )
| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
13.若关于x的方程nx2+(2n+1)x+n=0有实根,则n应满足条件( )
| A. | n≥-$\frac{1}{4}$,且n≠0 | B. | n≥-$\frac{1}{4}$ | C. | n≤-$\frac{1}{4}$ | D. | n≤-$\frac{1}{4}$,且n≠0 |
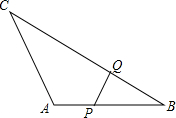 如图,在△ABC中,AB=8,BC=16,点P从点A开始沿AB向点B以2m/s的速度移动,点Q从点B开始沿BC向点C以4m/s的速度移动,如果P,Q分别从AB,BC同时出发,经过几秒△PBQ与△ABC相似?
如图,在△ABC中,AB=8,BC=16,点P从点A开始沿AB向点B以2m/s的速度移动,点Q从点B开始沿BC向点C以4m/s的速度移动,如果P,Q分别从AB,BC同时出发,经过几秒△PBQ与△ABC相似?