题目内容
8.在四边形ABCD中,对角线AC,BD交于点O,OA=OC,OB=OD,添加一个条件使四边形ABCD是矩形,那么所添加的条件可以是AC=BD或∠ABC=90°(写出一个即可).分析 先证明四边形ABCD是平行四边形,再由对角线相等或一个直角,即可得出四边形ABCD是矩形.
解答 解:添加的条件是:AC=BD或∠ABC=90°;理由如下:
∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
当AC=BD时,四边形ABCD是矩形(对角线相等的平行四边形是矩形);
当∠ABC=90°时,四边形ABCD是矩形(有一个角是直角的平行四边形是矩形).
故答案为:AC=BD或∠ABC=90°.
点评 本题考查了平行四边形的判定、矩形的判定方法;熟练掌握平行四边形和菱形的判定方法,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
18.两数相加,和小于每一个加数,那么这两个数是( )
| A. | 同为正数 | B. | 同为负数 | ||
| C. | 一正一负 | D. | 一个为0,另一个为正 |

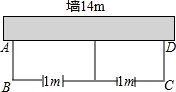 如图,有长为22米的篱笆,一面利用墙(墙的最大可用长度为14米),围成中间隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圃时,在BC上用其他材料造了宽为1米的两个小门.
如图,有长为22米的篱笆,一面利用墙(墙的最大可用长度为14米),围成中间隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圃时,在BC上用其他材料造了宽为1米的两个小门.