题目内容
7. 如图,点C的坐标为(3,y),使△ABC的周长最短,求y的值.
如图,点C的坐标为(3,y),使△ABC的周长最短,求y的值.
分析 作出点A关于直线x=3的对称点A′,连接A′B交直线x=3与点C,先求得BA′的解析式,然后将x=3代入直线BA′的解析式,从而可求得y的值.
解答 解:作A关于x=3的对称点A′,连接A′B交直线x=3与点C.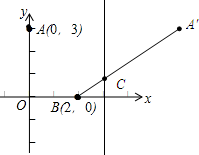
∵点A与点A′关于x=3对称,
∴AC=A′C.
∴AC+BC=A′C+BC.
当点B、C、A′在同一条直线上时,A′C+BC有最小值,即△ABC的周长有最小值.
∵点A与点A′关于x=3对称,
∴点A′的坐标为(6,3).
设直线BA′的解析式y=kx+b,将点B和点A′的坐标代入得:$\left\{\begin{array}{l}{2k+b=0}\\{6k+b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=-\frac{3}{2}}\end{array}\right.$.
∴y=$\frac{3}{4}x-\frac{3}{2}$.
将x=3代入函数的解析式得y=$\frac{3}{4}$.
∴y的值为$\frac{3}{4}$.
点评 本题主要考查的是轴对称路径最短、一次函数,明确当点B、C、A′在同一条直线上时,A′C+BC有最小值是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.下列各图是由若干盆花组成的形如正方形的图案,每条边上(包括两个顶点)有n(n>1)盆花,每个图案花盆的总数是s,按图所示的图案回答下列问题.

(1)填表:
(2)当n=10时,s的值是多少?s是如何随n的变化而变化的?

(1)填表:
| n | 2 | 3 | 4 | 5 | 6 | … | n |
| s | 4 | 9 | 16 | 25 | 36 | … | n2 |
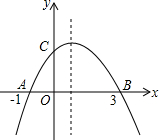 如图,二次函数y=ax2+bx+c的图象经过A (-1,0),B(3,0),C(0,3)两点.
如图,二次函数y=ax2+bx+c的图象经过A (-1,0),B(3,0),C(0,3)两点.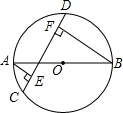 如图,AB是⊙O的直径,CD是⊙O的弦,AE⊥CD于E,BF⊥CD于F
如图,AB是⊙O的直径,CD是⊙O的弦,AE⊥CD于E,BF⊥CD于F 如图,把线段AB平移到线段A′B′,AB与A′B′平行吗?请说明理由.
如图,把线段AB平移到线段A′B′,AB与A′B′平行吗?请说明理由.