题目内容
17.三角形ABC,AB=13,BC=5,AC=12,则它的内切圆半径是3.分析 根据三角形三边长可判定三角形为直角三角形,从而可求得三角形ACB的面积,然后根据三角形ABC的面积=$\frac{1}{2}×$三角形ACB的周长×内切圆的半径求解即可.
解答 解:∵AB=13,BC=5,AC=12,
∴AB2=BC2+AC2.
∴△ABC为Rt△.
∴△ABC的面积=$\frac{1}{2}×5×12$=30.
根据三角形ABC的面积=$\frac{1}{2}×$三角形ACB的周长×内切圆的半径可知:$\frac{1}{2}×(13+5+12)r=30$,
解得:r=3.
故答案为:3.
点评 本题主要考查的是勾股定理的逆定理的应用、三角形的面积公式,明确三角形ABC的面积=$\frac{1}{2}×$三角形ACB的周长×内切圆的半径是解题的关键.

练习册系列答案
相关题目
12.下列算结果正确的是( )
| A. | -8-(-3)=5 | B. | (-2.5)-(+7.2)=4.7 | C. | (-$\frac{2}{5}$)-(-$\frac{1}{4}$)=-$\frac{3}{20}$ | D. | 5-(-6)=-1 |
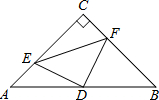 如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E,F分别在AC,BC边上运动(点E不与点A,C重合),且保持ED⊥FD,连接DE,DF,EF,在此运动变化的过程中,有下列结论:
如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E,F分别在AC,BC边上运动(点E不与点A,C重合),且保持ED⊥FD,连接DE,DF,EF,在此运动变化的过程中,有下列结论: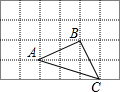 如图是单位长度为1的正方形网格,点A、B、C都在格点上;
如图是单位长度为1的正方形网格,点A、B、C都在格点上;
 如图,点C的坐标为(3,y),使△ABC的周长最短,求y的值.
如图,点C的坐标为(3,y),使△ABC的周长最短,求y的值.