题目内容
 如图,在Rt△ABC中,∠C=90°,AC=BC=m,延长CA到D,使AD=AB,连接BD.
如图,在Rt△ABC中,∠C=90°,AC=BC=m,延长CA到D,使AD=AB,连接BD.(1)求∠D的度数和它的正切值;
(2)利用上面的结果计算:tan22.5°-sin45°+
| (cos45°-tan22.5°)2 |
考点:解直角三角形,特殊角的三角函数值
专题:
分析:(1)根据AD=AB可求得∠D的值,再根据CD和BC的值即可求得tanD的值;
(2)根据sin45°=
,cos45°=
,将tan22.5°的值代入即可解题.
(2)根据sin45°=
| ||
| 2 |
| ||
| 2 |
解答:解:(1)∵在Rt△ABC中,∠C=90°,AC=BC=m,
∴AB=
m,∠BAC=45°,
∵∠D+∠DBA=∠BAC=45°,
∴∠D=22.5°,
∴tanD=
=
=
-1;
(2)由(1)得:tan22.5°=
-1,
∴tan22.5°-sin45°+
=
-1-
+|cos45°-tan22.5°|
=
-1-
+1-
=0.
∴AB=
| 2 |
∵∠D+∠DBA=∠BAC=45°,
∴∠D=22.5°,
∴tanD=
| BC |
| CD |
| m | ||
(
|
| 2 |
(2)由(1)得:tan22.5°=
| 2 |
∴tan22.5°-sin45°+
| (cos45°-tan22.5°)2 |
=
| 2 |
| ||
| 2 |
=
| 2 |
| ||
| 2 |
| ||
| 2 |
=0.
点评:本题考查了直角三角中正切值的计算,考查了特殊角的三角函数值,本题中求得
的值是解题的关键.
| BC |
| CD |

练习册系列答案
相关题目
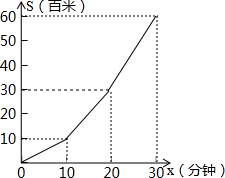 小明利用星期六、日双休骑自行车到城外小姨家去玩,星期六从家中出发,先上坡,后走平路,再走下坡路到小姨家,行程情况如图所示.星期日小明又沿原路返回自己家中,小明上坡、平路、下坡行驶的速度相对不变,则星期日,小明返回家的时间是( )
小明利用星期六、日双休骑自行车到城外小姨家去玩,星期六从家中出发,先上坡,后走平路,再走下坡路到小姨家,行程情况如图所示.星期日小明又沿原路返回自己家中,小明上坡、平路、下坡行驶的速度相对不变,则星期日,小明返回家的时间是( )| A、30分钟 | ||
B、38
| ||
C、41
| ||
D、43
|
 已知:如图,CB=DE,∠B=∠E,∠BAE=∠CAD.
已知:如图,CB=DE,∠B=∠E,∠BAE=∠CAD. 如图,将△ABC放在每个小正方形面积为1的网格中,点A、B、C均落在格点上,则△ABC的面积为
如图,将△ABC放在每个小正方形面积为1的网格中,点A、B、C均落在格点上,则△ABC的面积为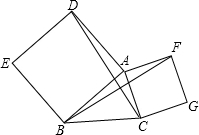 以△ABC的AB、AC为边分别作正方形ADEB、ACGF,连接DC、BF.
以△ABC的AB、AC为边分别作正方形ADEB、ACGF,连接DC、BF.