题目内容
 已知:如图,CB=DE,∠B=∠E,∠BAE=∠CAD.
已知:如图,CB=DE,∠B=∠E,∠BAE=∠CAD.求证:AC=AD.
考点:全等三角形的判定与性质
专题:证明题
分析:易证∠BAC=∠EAD,即可证明△ABC≌△AED,即可解题.
解答:解:∵∠BAE=∠CAD
∴∠BAE-∠CAE=∠CAD-∠CAE
∴∠BAC=∠EAD,
在△ABC与△AED中,
,
∴△ABC≌△AED(AAS),
∴AC=AD.
∴∠BAE-∠CAE=∠CAD-∠CAE
∴∠BAC=∠EAD,
在△ABC与△AED中,
|
∴△ABC≌△AED(AAS),
∴AC=AD.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ABC≌△AED是解题的关键.

练习册系列答案
相关题目
一个不透明的袋子中有5个白球、2个黄球和3个红球,这些球除颜色可以不同外其他完全相同,则从袋子中随机摸出一个球是黄球的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
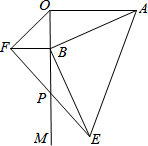 如图,AO⊥OM,OA=8
如图,AO⊥OM,OA=8| 2 |
| A、4 | ||
B、4
| ||
C、6
| ||
| D、BP的长度随B点的运动而变化 |
把抛物线y=-x2的图象向左平移2个单位,再向上平移3个单位,所得的抛物线的函数关系是( )
| A、y=-x2+2 |
| B、y=-x2+1 |
| C、y=-( x-2)2+1 |
| D、y=-( x+2)2+3 |
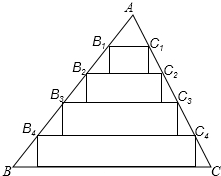 给一版墙镶边,需要4cm宽的彩色纸条48cm.现有如图一张三角形彩色纸零件,其中BC=25cm,BC边上的高线长为20cm.小慧给出一种裁纸方法:如图,将AB、AC分别五等分,然后连结两边对应的点,并以这些连结线为一边作矩形.剪下矩形纸条作为墙报镶边的材料.问:小慧的这种方法能满足这版墙报镶边的需要吗?请说明理由.
给一版墙镶边,需要4cm宽的彩色纸条48cm.现有如图一张三角形彩色纸零件,其中BC=25cm,BC边上的高线长为20cm.小慧给出一种裁纸方法:如图,将AB、AC分别五等分,然后连结两边对应的点,并以这些连结线为一边作矩形.剪下矩形纸条作为墙报镶边的材料.问:小慧的这种方法能满足这版墙报镶边的需要吗?请说明理由. 如图:AC=DB,AB=DC,求证:∠A=∠D.
如图:AC=DB,AB=DC,求证:∠A=∠D. 如图,在Rt△ABC中,∠C=90°,AC=BC=m,延长CA到D,使AD=AB,连接BD.
如图,在Rt△ABC中,∠C=90°,AC=BC=m,延长CA到D,使AD=AB,连接BD.