题目内容
如图，将△ABC放在每个小正方形面积为1的网格中，点A、B、C均落在格点上，则△ABC的面积为考点：等腰直角三角形
专题：网格型
分析：根据△ABC在网格中位置可以求得AB，BC，AC的值，可判定△ABC为等腰直角三角形，即可求得△ABC面积．
解答：解：BA=
=
，
BC=
=
，
AC=
=
，
∵AB2+BC2=AC2，
∴△ABC为等腰直角三角形，
∴△ABC面积=
AB•BC=2.5，
故答案为2.5．
| 12+22 |
| 5 |
BC=
| 12+22 |
| 5 |
AC=
| 12+32 |
| 10 |
∵AB2+BC2=AC2，
∴△ABC为等腰直角三角形，
∴△ABC面积=
| 1 |
| 2 |
故答案为2.5．
点评：本题考查了等腰直角三角形的判定，考查了直角三角形面积的计算，本题中求得AB2+BC2=AC2是解题的关键．
练习册系列答案
相关题目
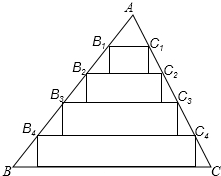给一版墙镶边，需要4cm宽的彩色纸条48cm．现有如图一张三角形彩色纸零件，其中BC=25cm，BC边上的高线长为20cm．小慧给出一种裁纸方法：如图，将AB、AC分别五等分，然后连结两边对应的点，并以这些连结线为一边作矩形．剪下矩形纸条作为墙报镶边的材料．问：小慧的这种方法能满足这版墙报镶边的需要吗？请说明理由．
如图：AC=DB，AB=DC，求证：∠A=∠D．
已知：如图，在△ABC中，CD⊥AB于D，BE⊥AC于E，AD=AE．求证：AB=AC．
如图，在Rt△ABC中，∠C=90°，AC=BC=m，延长CA到D，使AD=AB，连接BD．