题目内容
18.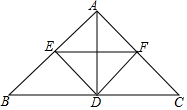 如图,在△ABC中,AB=AC,D是边BC上的一点,DE⊥AB,DF⊥AC,垂足分别是E、F,EF∥BC.
如图,在△ABC中,AB=AC,D是边BC上的一点,DE⊥AB,DF⊥AC,垂足分别是E、F,EF∥BC.(1)求证:△BDE≌△CDF;
(2)若BC=2AD,求证:四边形AEDF是正方形.
分析 (1)首先证明AE=AF,推出BE=CF,根据ASA即可证明.
(2)首先证明殊不知AEDF是矩形,再由邻边相等推出是正方形.
解答 证明:(1)∵AB=AC,
∴∠B=∠C,
∵EF∥BC,
∴∠AEF=∠B,∠AFE=∠C,
∴∠AEF=∠AFE,
∴AE=AF,
∴BE=CF,
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°,
在△BED和△CFD中,
$\left\{\begin{array}{l}{∠BED=∠DFC}\\{BE=CF}\\{∠B=∠C}\end{array}\right.$,
∴△BDE≌△CDF.
(2)∵△BDE≌△CDF,
∴BD=DC,DE=DF,
∵BC=2AD,
∴AD=$\frac{1}{2}$BC,
∴∠BAC=90°,
∵DE⊥AB,DF⊥AC,
∴∠EAF=∠AED=∠AFD=90°,
∴四边形AEDF是矩形,
∵AE=AF,
∴四边形AEDF是正方形.
点评 本题考查全等三角形的判定和性质、正方形的判定、直角三角形的判定、平行线的性质等知识,解题的关键是正确寻找全等条件,熟练应用所学知识解决问题,属于中考常考题型.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
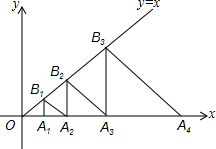 如图,△A1B1A2,A2B2A3,A3B3A4,…,AnBnAn+1都是等腰直角三角形,其中点A1、A2、…、An在x轴上,点B1、B2、…、Bn在直线y=x上,已知OA2=1,则OA2017的长为22015.
如图,△A1B1A2,A2B2A3,A3B3A4,…,AnBnAn+1都是等腰直角三角形,其中点A1、A2、…、An在x轴上,点B1、B2、…、Bn在直线y=x上,已知OA2=1,则OA2017的长为22015. 如图,在矩形ABCD中,对角线AC、BD相交于点O,若AE平分∠BAD交BC于点E,且BO=BE,连接OE,则∠BOE=75°.
如图,在矩形ABCD中,对角线AC、BD相交于点O,若AE平分∠BAD交BC于点E,且BO=BE,连接OE,则∠BOE=75°. 如图,在矩形ABCD中,点E是BC上一点,且DE=DA,AF⊥DE于F,求证:AF=CD.
如图,在矩形ABCD中,点E是BC上一点,且DE=DA,AF⊥DE于F,求证:AF=CD. 如图,小明要测量河内小岛B到河边公路AD的距离,在点A处测得∠BAD=37°,沿AD方向前进150米到达点C,测得∠BCD=45°.求小岛B到河边公路AD的距离.
如图,小明要测量河内小岛B到河边公路AD的距离,在点A处测得∠BAD=37°,沿AD方向前进150米到达点C,测得∠BCD=45°.求小岛B到河边公路AD的距离.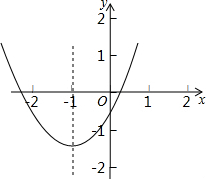 已知抛物线y=ax2+bx+c(a>0)的对称轴为直线x=-1,该抛物线与x轴的一个交点为(x1,0),且0<x1<1,有下列结论:①abc>0;②9a-3b+c>0;③b<a;④3a+c>0.其中正确结论的个数是( )
已知抛物线y=ax2+bx+c(a>0)的对称轴为直线x=-1,该抛物线与x轴的一个交点为(x1,0),且0<x1<1,有下列结论:①abc>0;②9a-3b+c>0;③b<a;④3a+c>0.其中正确结论的个数是( )