题目内容
6.已知△ABC中,AB=AC,AB的垂直平分线交AB于点D,交直线AC于点E,若∠EBC=42°,则∠BAC的度数为32°或152°或88°.分析 根据等腰三角形的性质得到∠ABC=∠ACB,根据线段垂直平分线的性质得到EA=EB,得到∠ABE=∠A,根据三角形的外角的性质计算即可.
解答  解:如图1,∵△ABC是等腰三角形,
解:如图1,∵△ABC是等腰三角形,
∴∠ABC=∠ACB,∠ABC+∠ACB+∠A=180°,
∵DE垂直且平分AB,
∴EA=EB,
∴∠ABE=∠A,
∴∠EBC+∠ACB=∠AEB,
42°+$\frac{1}{2}$(180°-∠A)=180°-2∠A,
解得∠BAC=32°.
如图2,同理可得∠BAC=152°,
如图3, 同理可得∠BAC=88°,
同理可得∠BAC=88°,
综上所述∠BAC=32°或152°或88°,
故答案为:32°或152°或88°.
点评 本题考查的是线段垂直平分线的性质以及等腰三角形的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等.

练习册系列答案
相关题目
17.下列命题是真命题的是( )
| A. | 垂直于同一条直线的两条直线互相平行 | |
| B. | 同旁内角互补 | |
| C. | 若a2=b2,则|a|=|b| | |
| D. | 若a>0,则a2>a |
1.下列命题中,是真命题的是( )
| A. | 同位角相等 | |
| B. | 相等的角是对顶角 | |
| C. | 同角的余角相等 | |
| D. | 过一点有且只有一条直线与已知直线平行 |
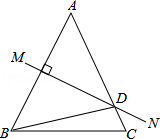 如图,等腰△ABC中,AB=AC,∠BAC=50°,AB的垂直平分线MN交AC于点D,则∠DBC的度数是15°.
如图,等腰△ABC中,AB=AC,∠BAC=50°,AB的垂直平分线MN交AC于点D,则∠DBC的度数是15°.
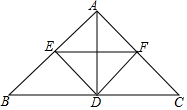 如图,在△ABC中,AB=AC,D是边BC上的一点,DE⊥AB,DF⊥AC,垂足分别是E、F,EF∥BC.
如图,在△ABC中,AB=AC,D是边BC上的一点,DE⊥AB,DF⊥AC,垂足分别是E、F,EF∥BC. 如图,在△ABC中,BD是∠ABC的平分线,EF垂直平分BD.
如图,在△ABC中,BD是∠ABC的平分线,EF垂直平分BD.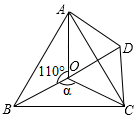 如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕着点C按顺时针方向旋转60°得到△ADC,连结OD,当α=150°时,△AOD是直角三角形.
如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕着点C按顺时针方向旋转60°得到△ADC,连结OD,当α=150°时,△AOD是直角三角形.