题目内容
10. 如图,在矩形ABCD中,点E是BC上一点,且DE=DA,AF⊥DE于F,求证:AF=CD.
如图,在矩形ABCD中,点E是BC上一点,且DE=DA,AF⊥DE于F,求证:AF=CD.
分析 根据已知及矩形的性质利用AAS判定△ADF≌△DEC,从而利用全等三角形的性质可得出要证明的结论.
解答 证明:∵AF⊥DE,
∴∠AFD=90°,
∵在矩形ABCD中,AD∥BC,
∴∠ADF=∠DEC,
在△ADF和△DEC中,$\left\{\begin{array}{l}{∠ADF=∠DEC}&{\;}\\{∠AFD=∠DCE}&{\;}\\{AD=DE}&{\;}\end{array}\right.$,
∴△ADF≌△DEC(AAS),
∴AF=CD.
点评 此题考查了矩形的性质、全等三角形的判定及性质,属于基础题,解答本题的关键是得出∠ADF=∠DEC,利用AAS证明△ADF≌△DEC,难度一般.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.下列命题中,是真命题的是( )
| A. | 同位角相等 | |
| B. | 相等的角是对顶角 | |
| C. | 同角的余角相等 | |
| D. | 过一点有且只有一条直线与已知直线平行 |
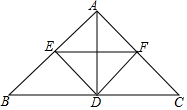 如图,在△ABC中,AB=AC,D是边BC上的一点,DE⊥AB,DF⊥AC,垂足分别是E、F,EF∥BC.
如图,在△ABC中,AB=AC,D是边BC上的一点,DE⊥AB,DF⊥AC,垂足分别是E、F,EF∥BC. 如图,在△ABC中,BD是∠ABC的平分线,EF垂直平分BD.
如图,在△ABC中,BD是∠ABC的平分线,EF垂直平分BD.