题目内容
7. 如图,小明要测量河内小岛B到河边公路AD的距离,在点A处测得∠BAD=37°,沿AD方向前进150米到达点C,测得∠BCD=45°.求小岛B到河边公路AD的距离.
如图,小明要测量河内小岛B到河边公路AD的距离,在点A处测得∠BAD=37°,沿AD方向前进150米到达点C,测得∠BCD=45°.求小岛B到河边公路AD的距离.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
分析 过B作BE⊥CD垂足为E,设BE=x米,再利用锐角三角函数关系得出AE=$\frac{4}{3}$x,CE=x,根据AC=AE-CE,得到关于x的方程,即可得出答案.
解答  解:过B作BE⊥CD垂足为E,设BE=x米,
解:过B作BE⊥CD垂足为E,设BE=x米,
在Rt△ABE中,tanA=$\frac{BE}{AE}$,
AE=$\frac{BE}{tanA}$=$\frac{BE}{tan37°}$=$\frac{4}{3}$x,
在Rt△ABE中,tan∠BCD=$\frac{BE}{CE}$,
CE=$\frac{BE}{tan∠BCD}$=$\frac{x}{tan45°}$=x,
AC=AE-CE,
$\frac{4}{3}$x-x=150,
x=450.
答:小岛B到河边公路AD的距离为450米.
点评 此题主要考查了解直角三角形的应用,解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
17.下列命题是真命题的是( )
| A. | 垂直于同一条直线的两条直线互相平行 | |
| B. | 同旁内角互补 | |
| C. | 若a2=b2,则|a|=|b| | |
| D. | 若a>0,则a2>a |
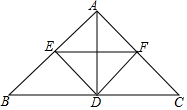 如图,在△ABC中,AB=AC,D是边BC上的一点,DE⊥AB,DF⊥AC,垂足分别是E、F,EF∥BC.
如图,在△ABC中,AB=AC,D是边BC上的一点,DE⊥AB,DF⊥AC,垂足分别是E、F,EF∥BC. 如图,在△ABC中,BD是∠ABC的平分线,EF垂直平分BD.
如图,在△ABC中,BD是∠ABC的平分线,EF垂直平分BD.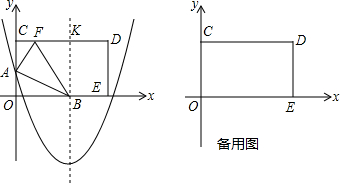
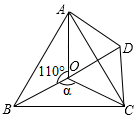 如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕着点C按顺时针方向旋转60°得到△ADC,连结OD,当α=150°时,△AOD是直角三角形.
如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕着点C按顺时针方向旋转60°得到△ADC,连结OD,当α=150°时,△AOD是直角三角形.