题目内容
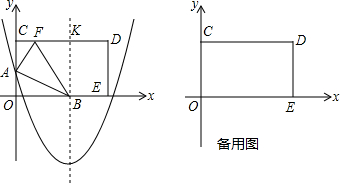
9. 如图,在矩形ABCD中,对角线AC、BD相交于点O,若AE平分∠BAD交BC于点E,且BO=BE,连接OE,则∠BOE=75°.
如图,在矩形ABCD中,对角线AC、BD相交于点O,若AE平分∠BAD交BC于点E,且BO=BE,连接OE,则∠BOE=75°.
分析 由矩形ABCD,得到OA=OB,根据AE平分∠BAD,得到等边三角形OAB,∠ABO=60°,求出∠OBE=30°,根据三角形的内角和定理即可求出答案.
解答 解:∵四边形ABCD是矩形,
∴AD∥BC,AC=BD,OA=OC,OB=OD,∠BAD=90°,
∴OA=OB,∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE=45°=∠AEB,
∴AB=BE,
∵BO=BE,
∴AB=BO=OA
∴△BAO是等边三角形,
∴∠ABO=60°,
∴∠OBE=90°-60°=30°,
OB=BE,
∴∠BOE=∠BEO=$\frac{1}{2}$(180°-30°)=75°.
故答案为75°.
点评 本题主要考查了三角形的内角和定理,矩形的性质,等边三角形的性质和判定,平行线的性质,角平分线的性质,等腰三角形的判定等知识点,解此题的关键是证明△BAO是等边三角形.

练习册系列答案
相关题目
19.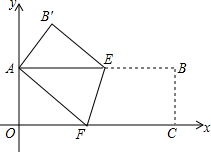 如图,矩形AOCB边OC在x轴上点B的坐标为(3,1),将此矩形折叠,使点C与点A重合,点B折至点B'处,折痕为EF,则点B'的坐标为($\frac{3}{5}$,$\frac{9}{5}$).
如图,矩形AOCB边OC在x轴上点B的坐标为(3,1),将此矩形折叠,使点C与点A重合,点B折至点B'处,折痕为EF,则点B'的坐标为($\frac{3}{5}$,$\frac{9}{5}$).
 如图,矩形AOCB边OC在x轴上点B的坐标为(3,1),将此矩形折叠,使点C与点A重合,点B折至点B'处,折痕为EF,则点B'的坐标为($\frac{3}{5}$,$\frac{9}{5}$).
如图,矩形AOCB边OC在x轴上点B的坐标为(3,1),将此矩形折叠,使点C与点A重合,点B折至点B'处,折痕为EF,则点B'的坐标为($\frac{3}{5}$,$\frac{9}{5}$).
17.下列命题是真命题的是( )
| A. | 垂直于同一条直线的两条直线互相平行 | |
| B. | 同旁内角互补 | |
| C. | 若a2=b2,则|a|=|b| | |
| D. | 若a>0,则a2>a |
1.下列命题中,是真命题的是( )
| A. | 同位角相等 | |
| B. | 相等的角是对顶角 | |
| C. | 同角的余角相等 | |
| D. | 过一点有且只有一条直线与已知直线平行 |
 直线y=kx+b如图,则关于x的不等式kx+b≤-2的解集是x≥-1.
直线y=kx+b如图,则关于x的不等式kx+b≤-2的解集是x≥-1.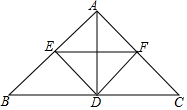 如图,在△ABC中,AB=AC,D是边BC上的一点,DE⊥AB,DF⊥AC,垂足分别是E、F,EF∥BC.
如图,在△ABC中,AB=AC,D是边BC上的一点,DE⊥AB,DF⊥AC,垂足分别是E、F,EF∥BC.