题目内容
8.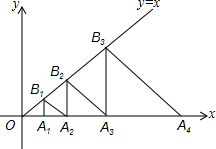 如图,△A1B1A2,A2B2A3,A3B3A4,…,AnBnAn+1都是等腰直角三角形,其中点A1、A2、…、An在x轴上,点B1、B2、…、Bn在直线y=x上,已知OA2=1,则OA2017的长为22015.
如图,△A1B1A2,A2B2A3,A3B3A4,…,AnBnAn+1都是等腰直角三角形,其中点A1、A2、…、An在x轴上,点B1、B2、…、Bn在直线y=x上,已知OA2=1,则OA2017的长为22015.
分析 根据规律得出OA1=$\frac{1}{2}$,OA2=1,OA3=2,OA4=4,所以可得OAn=2n-2,进而解答即可.
解答 解:∵OA2=1,
∴OA1=$\frac{1}{2}$,OA2=1,OA3=2,OA4=4,
∴OAn=2n-2,
∴OA2017=22015,
故答案为:22015.
点评 此题考查一次函数图象上点的坐标,关键是根据规律得出OAn=2n-2进行解答.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
18.计算-5-(-2)×3的结果等于( )
| A. | -11 | B. | -1 | C. | 1 | D. | 11 |
19.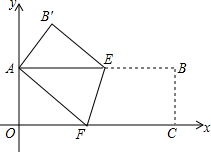 如图,矩形AOCB边OC在x轴上点B的坐标为(3,1),将此矩形折叠,使点C与点A重合,点B折至点B'处,折痕为EF,则点B'的坐标为($\frac{3}{5}$,$\frac{9}{5}$).
如图,矩形AOCB边OC在x轴上点B的坐标为(3,1),将此矩形折叠,使点C与点A重合,点B折至点B'处,折痕为EF,则点B'的坐标为($\frac{3}{5}$,$\frac{9}{5}$).
 如图,矩形AOCB边OC在x轴上点B的坐标为(3,1),将此矩形折叠,使点C与点A重合,点B折至点B'处,折痕为EF,则点B'的坐标为($\frac{3}{5}$,$\frac{9}{5}$).
如图,矩形AOCB边OC在x轴上点B的坐标为(3,1),将此矩形折叠,使点C与点A重合,点B折至点B'处,折痕为EF,则点B'的坐标为($\frac{3}{5}$,$\frac{9}{5}$).
17.下列命题是真命题的是( )
| A. | 垂直于同一条直线的两条直线互相平行 | |
| B. | 同旁内角互补 | |
| C. | 若a2=b2,则|a|=|b| | |
| D. | 若a>0,则a2>a |
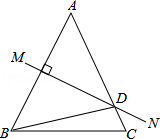 如图,等腰△ABC中,AB=AC,∠BAC=50°,AB的垂直平分线MN交AC于点D,则∠DBC的度数是15°.
如图,等腰△ABC中,AB=AC,∠BAC=50°,AB的垂直平分线MN交AC于点D,则∠DBC的度数是15°.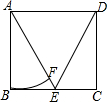 如图,在矩形ABCD中,点E在边BC上,BE=EC=2,且AE=AD,以A为圆心,AB长为半径作圆弧AE于点F,则扇形ABF的面积是π(结果保留π).
如图,在矩形ABCD中,点E在边BC上,BE=EC=2,且AE=AD,以A为圆心,AB长为半径作圆弧AE于点F,则扇形ABF的面积是π(结果保留π). 如图,点D、E分别是△ABC的边AC、BC上的点,AD=DE,AB=BE,∠A=80°,则∠BED=80°.
如图,点D、E分别是△ABC的边AC、BC上的点,AD=DE,AB=BE,∠A=80°,则∠BED=80°. 如图,在△ABC中,AB=AC,D是边BC上的一点,DE⊥AB,DF⊥AC,垂足分别是E、F,EF∥BC.
如图,在△ABC中,AB=AC,D是边BC上的一点,DE⊥AB,DF⊥AC,垂足分别是E、F,EF∥BC.