题目内容
1. 如图,四边形ABCD与CEFG都是菱形,点B,C,E在同一直线上,∠ADC=∠GCE=60°,点H为AF的中点,则$\frac{DH}{HG}$的值为( )
如图,四边形ABCD与CEFG都是菱形,点B,C,E在同一直线上,∠ADC=∠GCE=60°,点H为AF的中点,则$\frac{DH}{HG}$的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
分析 如图,延长DH使得HM=DH,连接AM、DF,MF,只要证明MG=DG,∠DHG=90°,∠HDG=30°,即可解决问题.
解答 解:如图,延长DH使得HM=DH,连接AM、DF,MF.
∵AH=FH,HM=HD,
∴四边形AMFD是平行四边形,
∴AD∥FM,AD=MF,
∵四边形ABCD与CEFG都是菱形,
∴AD∥BE,GF∥BE,AD=CD,CG=GF,
∴FG∥AD,
∴F、G、M共线,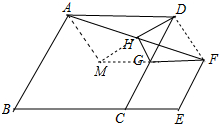
∴FM=CD,∵CG=GF,
∴GM=GD,
∵HM=HD,
∴GH⊥DM,∠GMD=∠MDG=∠ADM=30°
∴∠DHG=90°,
∴tan30°=$\frac{HG}{DH}$=$\frac{\sqrt{3}}{3}$,
∴$\frac{DH}{HG}$=$\sqrt{3}$,
故选D.
点评 本题考查菱形的判定和性质、平行四边形的判定和性质、等腰三角形的判定和性质、锐角三角函数等知识,解题的关键是添加辅助线,构造特殊四边形解决问题,属于中考常考题型.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
3.下列四个几何体中,主视图为圆的是( )
| A. |  | B. |  | C. |  | D. |  |
12.与3-$\sqrt{0.5}$的和是有理数的是( )
| A. | $\frac{1}{10}\sqrt{5}$ | B. | 2$\sqrt{\frac{1}{8}}$ | C. | $\sqrt{\frac{2}{5}}$ | D. | 3+$\sqrt{5}$ |
9.下列说法正确的是( )
| A. | x2y3z没有系数 | B. | (x-1)0的值是1 | ||
| C. | 2016π是一次单项式 | D. | x4+x3y2+1是五次三项式 |
6.下列数值中,不是不等式$\frac{5}{2}$x≥2(x-3)+3的解的是( )
| A. | -7 | B. | -6 | C. | -5 | D. | -4 |
13. 如图,在矩形ABCD中,连接BD,将△ABD沿BD进行折叠,使得点A落到点M处,DM交BC于点N,若AB=2,BD=5,则MN的长度为( )
如图,在矩形ABCD中,连接BD,将△ABD沿BD进行折叠,使得点A落到点M处,DM交BC于点N,若AB=2,BD=5,则MN的长度为( )
 如图,在矩形ABCD中,连接BD,将△ABD沿BD进行折叠,使得点A落到点M处,DM交BC于点N,若AB=2,BD=5,则MN的长度为( )
如图,在矩形ABCD中,连接BD,将△ABD沿BD进行折叠,使得点A落到点M处,DM交BC于点N,若AB=2,BD=5,则MN的长度为( )| A. | $\frac{17\sqrt{21}}{42}$ | B. | $\frac{17\sqrt{21}}{21}$ | C. | 17$\sqrt{21}$ | D. | 34$\sqrt{21}$ |