题目内容
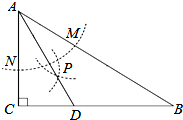 如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心,大于
如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心,大于| 1 |
| 2 |
考点:作图—基本作图,角平分线的性质,线段垂直平分线的性质
专题:
分析:①根据作图的过程可以判定AD是∠BAC的角平分线;
②利用角平分线的定义可以推知∠CAD=30°,则由直角三角形的性质来求∠ADC的度数;
③利用等角对等边可以证得△ADB的等腰三角形,由等腰三角形的“三合一”的性质可以证明点D在AB的中垂线上;
④利用30度角所对的直角边是斜边的一半、三角形的面积计算公式来求两个三角形的面积之比.
②利用角平分线的定义可以推知∠CAD=30°,则由直角三角形的性质来求∠ADC的度数;
③利用等角对等边可以证得△ADB的等腰三角形,由等腰三角形的“三合一”的性质可以证明点D在AB的中垂线上;
④利用30度角所对的直角边是斜边的一半、三角形的面积计算公式来求两个三角形的面积之比.
解答: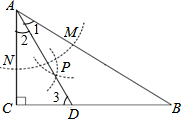 解:①根据作图的过程可知,AD是∠BAC的平分线.
解:①根据作图的过程可知,AD是∠BAC的平分线.
故①正确;
②如图,∵在△ABC中,∠C=90°,∠B=30°,
∴∠CAB=60°.
又∵AD是∠BAC的平分线,
∴∠1=∠2=
∠CAB=30°,
∴∠3=90°-∠2=60°,即∠ADC=60°.
故②正确;
③∵∠1=∠B=30°,
∴AD=BD,
∴点D在AB的中垂线上.
故③正确;
④∵如图,在直角△ACD中,∠2=30°,
∴CD=
AD,
∴BC=CD+BD=
AD+AD=
AD,S△DAC=
AC•CD=
AC•AD.
∴S△ABD=
AC•BD=
AC•AD=
AC•AD,
∴S△DAC:S△ABD=
AC•AD:
AC•AD=1:2.
故④正确.
综上所述,正确的结论是:①②③④.
故答案为:①②③④.
 解:①根据作图的过程可知,AD是∠BAC的平分线.
解:①根据作图的过程可知,AD是∠BAC的平分线.故①正确;
②如图,∵在△ABC中,∠C=90°,∠B=30°,
∴∠CAB=60°.
又∵AD是∠BAC的平分线,
∴∠1=∠2=
| 1 |
| 2 |
∴∠3=90°-∠2=60°,即∠ADC=60°.
故②正确;
③∵∠1=∠B=30°,
∴AD=BD,
∴点D在AB的中垂线上.
故③正确;
④∵如图,在直角△ACD中,∠2=30°,
∴CD=
| 1 |
| 2 |
∴BC=CD+BD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
∴S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S△DAC:S△ABD=
| 1 |
| 4 |
| 1 |
| 2 |
故④正确.
综上所述,正确的结论是:①②③④.
故答案为:①②③④.
点评:本题考查了角平分线的性质、线段垂直平分线的性质以及作图-基本作图.解题时,需要熟悉等腰三角形的判定与性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
根据下列已知条件,能唯一画出△ABC的是( )
| A、AB=3,BC=4,AC=8 |
| B、∠C=90°,AB=6 |
| C、AB=3,BC=3,∠C=30° |
| D、∠A=60°,∠B=45°,AB=4 |
分别以下列四组数为一个三角形的三边长:①1、2、3;②2、3、4;③3、4、5;④4、5、6;其中能构成直角三角形的有( )
| A、1组 | B、2组 | C、3组 | D、4组 |
用反证法证明命题“三角形的内角中至少有一个不大于60度”,应先假设( )
| A、三个内角都不大于60度 |
| B、三个内角都大于60度 |
| C、三个内角至多有一个大于60度 |
| D、假设三内角至多有一个不大于60度 |
下列语句中不是命题的有( )
①两点之间,直线最短;②不许大声说话;③连接A、B两点;④花儿在春天开放.
①两点之间,直线最短;②不许大声说话;③连接A、B两点;④花儿在春天开放.
| A、1个 | B、2个 | C、3个 | D、4个 |
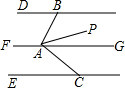 如图,已知DB∥FG∥EC,∠ABD=70°,∠ACE=34°,AP是∠BAC的平分线,求∠PAG.
如图,已知DB∥FG∥EC,∠ABD=70°,∠ACE=34°,AP是∠BAC的平分线,求∠PAG. 如图,AB∥CD,∠B=60°,∠D=55°,则∠O=
如图,AB∥CD,∠B=60°,∠D=55°,则∠O=